Tablas de distribución de frecuencias

A menudo disponemos de una vasta cantidad de datos provenientes de experimentos o encuestas, pero necesitamos en realidad conocer la información que estos datos nos puedan aportar. En estos casos, las tablas de frecuencias son una herramienta estadística de gran utilidad ya que nos permiten agrupar y ordenar los datos para su posterior análisis.

Frecuencias

La frecuencia estadística indica la cantidad de veces que se presenta un dato en una determinada muestra.

Frecuencia absoluta (f_i): Es la cantidad de veces que aparece un determinado valor, y lo denotamos con f_i, donde el subíndice indica cada uno de los valores. Si sumamos todas las frecuencias absolutas, obtendremos la cantidad total de datos que se denotas con N.

$N = f_{1} + f_{2} + f_{3} + ... + f_{n}$

Es decir,

$N = \sum_{i=1}^{n}f_{i}$

Frecuencia relativa ( $n_{i}$ ): Como su nombre lo indica, es una frecuencia que expresa la presencia de cada dato en relación con la cantidad total de datos. Se obtiene al dividir la frecuencia absoluta de cada valor entre la cantidad total de datos.

$n_{i} = \frac{f_{i}}{N}$

¿Sabías qué?

Si sumamos los valores de todas las frecuencias relativas, el resultado es 1.

Frecuencia acumulada ( $F_{i}$ ): Representa la suma de todas las frecuencias absolutas de los valores iguales o menores al valor considerado.

Tablas con frecuencia absoluta, relativa y acumulada

A partir de un conjunto de datos estadísticos, podemos elaborar un arreglo tabular donde se muestren las frecuencias con que se presenta cada atributo o característica en las que se han agrupado los datos.

La frecuencia relativa porcentual se determina cuando deseamos conocer la participación porcentual de una frecuencia respecto al total de valores. Se obtiene multiplicando la frecuencia relativa por 100.

Ejemplo

Se realizó una encuesta a 15 personas donde se les solicitó que indicaran cuál era su fruta favorita. Los resultados se muestran en la siguiente tabla:

Sujeto	Fruta favorita
1	Banana
2	Fresa
3	Banana
4	Parchita (maracuyá)
5	Piña (ananá)
6	Mora
7	Fresa
8	Mango
9	Melocotón
10	Naranja
11	Banana
12	Fresa
13	Piña (ananá)
14	Melocotón
15	Fresa

La correspondiente tabla de distribución de frecuencias será:

Fruta preferida	Frecuencia absoluta ( $f_{i}$ )	Frecuencia relativa ( $n_{i}$ )	Frecuencia acumulada ( $F_{i}$ )
Banana	3	$\frac{3}{15}$	3
Fresa	4	$\frac{4}{15}$	7
Parchita (maracuyá)	1	$\frac{1}{15}$	8
Piña (ananá)	2	$\frac{2}{15}$	10
Mora	1	$\frac{1}{15}$	11
Mango	1	$\frac{1}{15}$	12
Naranja	1	$\frac{1}{15}$	13
Melocotón	2	$\frac{2}{15}$	15
$\sum$	15	1	–

Clases

Las clases son los distintos intervalos de valores tomados en la construcción de una distribución. En las variables de tipo cualitativas, las clases ya se encuentran definidas, por ejemplo, color (negro, blanco, rojo, amarillo, verde…), tamaño (pequeño, grande, mediano), género (masculino, femenino). En el caso de las variables cuantitativas, las clases deben ser explícitamente definidas a partir de los intervalos de clases.

Intervalos de clase

Los intervalos de clases se refieren a cada rango de valores en que se hayan clasificado parcialmente los datos con la finalidad de hacer un resumen de ellos.

Marca de clase (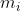 $m_{i}$ ):

También se le conoce como punto medio de clase. Es considerado el punto medio del intervalo de la clase. Su valor se calcula al promediar los extremos del intervalo.

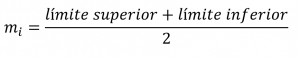
Los Histogramas

para muchas personas, la información representada en un gráfico suele tener mayor impacto y es más sencilla de entender que aquella presentada a modo de texto o tablas. En esos casos, siempre es conveniente complementar la información presentada en las tablas de frecuencias con el correspondiente histograma.

Los histogramas son representaciones gráficas de datos agrupados en intervalos. Su representación está formada por un conjunto de barras rectangulares, usualmente verticales, donde su longitud es equivalente a las frecuencias absolutas de cada una de los intervalos, aunque también podemos graficar las frecuencias relativas.