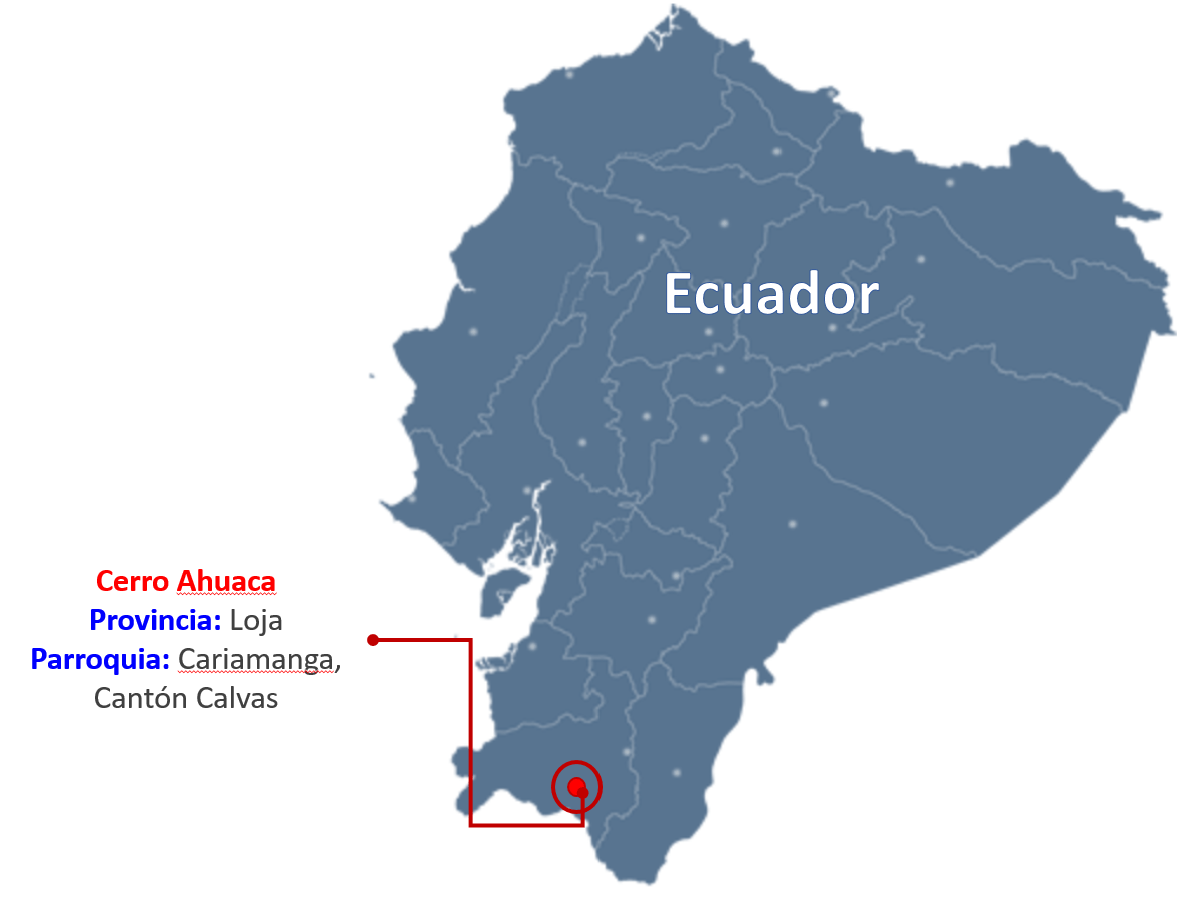
Se trata de un roedor que habita en el sur de Ecuador. También se le conoce como Vizcacha del cerro Ahuaca, y es una especie endémica que únicamente ha sido observada en la provincia de Loja, en el Cerro el Ahuaca, por lo que se conoce muy poco de su comportamiento y hábitos. Su reducido territorio y los pocos ejemplares que han sido avistados ubican a esta especie en la categoría de peligro crítico de extinción.

Ficha técnica
- Nombre común: Vizcacha del cerro Ahuaca
- Reino: Animalia
- Filo: Chordata
- Clase: Mammalia
- Orden: Rodentia
- Familia: Chinchillidae
- Género: Lagidium
- Especie: L. ahuacaense
- Tamaño: entre 30 y 60 cm
- Peso: aproximadamente 1,5 kg
- Estado de conservación: en peligro crítico de extinción
Características
La palabra Lagidium proviene del griego antiguo y significa liebre pequeña. Esto se debe a su parecido a una liebre aunque con diversas características que se distinguen: poseen un color marrón grisáceo en el lomo y gris amarillento en la zona ventral. Las orejas y cola son de un color negruzco.
Sus palmas y plantas se encuentran desprovistas de pelos y su cola tiene pelos largos de color café o tonos crema en la parte dorsal y más cortos y oscuros en la parte inferior de la cola.
La cola de este animal es un rasgo característico que no solo lo distingue de los conejos (Leporidae) y lo ubica en la familia de las chinchillas (Chinchillidae), sino que además denota si la vizcacha se encuentra ansiosa (la cola se extiende) o relajada (la cola está encorvada).
Tan solo en el año 2005 un grupo de investigadores liderados por Florian Werner observaron a esta especie y en el diciembre de 2006 publicaron en la revista de Mastozoología Neotropical los primeros hallazgos. En esa oportunidad, el roedor fue clasificado como una vizcacha, siendo la primera vez que se observaba este roedor en esa región de Ecuador, mientras que en Perú, Chile y Argentina son más comunes.
Finalmente, en el 2009, diversos estudios morfológicos, zoológicos y de ADN apuntan a que se trata de una especie con una divergencia significativa de sus parientes de Perú y otras regiones de Suramérica que ha evolucionado por aislamiento geográfico para formar una especie independiente.
Hábitat
Esta especie herbívora habita únicamente en el Cerro Ahuaca, el cual está formado por montañas de granito con empinadas pendientes que van de 40º a 90º a una altitud de entre 1.950 y 2.480 m s. n. m. con una vegetación de matorral seco montano. Los científicos Werner, Ledesma, Spotorno y Albuja en el 2006 observaron un grupo familiar constituido por dos adultos y dos jóvenes y notaron que el grupo en cuestión permanece en un radio de 2 metros alrededor de la cueva, aunque aún se desconocen muchos detalles del comportamiento de este animal.




 VOLVER A LOS ARTÍCULOS
VOLVER A LOS ARTÍCULOS