La teoría combinatoria se ocupa del ordenamiento de los elementos de un conjunto o su agrupación según varias leyes. Cuenta con fórmulas que permiten calcular el número de ordenaciones o la cantidad de grupos que pueden formarse. Las agrupaciones pueden clasificarse según diversas condiciones, teniendo en cuenta si sus elementos se repiten o no, cuántos de ellos se pueden tomar y si importa el orden de colocación.

Uno de los principios fundamentales que participan en la teoría combinatoria indica que:
Si algo se puede hacer de “p” maneras distintas, luego de haber hecho eso de una de las maneras quedan disponibles “q” maneras distintas para hacer otra cosa.
Es decir, como para cada una de las “p” maneras de realizar la primer cosa hay “q” maneras para realizar la segunda, el total de formas en las que ambas pueden hacerse es:
EJEMPLO: si una persona tiene 3 pantalones y 5 camisas, ¿de cuántas formas puede usar un pantalón y una camisa?
Cada pantalón se puede usar con cada una de las 5 camisas, por lo tanto tiene 3⋅5=15 formas de combinar un pantalón y una camisa.
PERMUTACIONES, VARIACIONES Y COMBINACIONES
Dada cierta cantidad de elementos, hay distintos criterios para determinar las formas de agrupación que éstos pueden tener y las consideraciones que diferencian a un grupo de otro.

Combinaciones (ordinarias)
Se denominan combinaciones de m elementos tomados de n en n a los grupos que pueden formase con esos m elementos, teniendo en cuenta que dos grupos se consideran diferentes únicamente cuando tienen algún elemento diferente.
La notación para las combinaciones es: ![]()
Fórmula: ![]()
EJEMPLO:
¿Cuántos grupos pueden formarse con los 4 elementos A, B, C y D tomados de tres en tres?
La totalidad de elementos es 4, por lo tanto m=4.
La cantidad de elementos por grupo es 3, entonces n=3.
Se aplica la fórmula:

Los grupos serían: ABC, ABD, ACD, ACD.
El factorial de un número entero positivo es el producto de todos los números naturales desde dicho número hasta 1. Ejemplo:
4!=4⋅3⋅2⋅1 = 24
Variaciones (ordinarias)
Se denominan variaciones de m elementos tomados de n en n a los grupos que se pueden formar con m elementos dados. Dos grupos se consideran distintos cuando difieren en algún elemento o cuando el orden de los elementos cambia.
En el ejemplo anterior no importa el orden de los elementos, por ello, para las combinaciones es lo mismo que el grupo esté conformado por ABC, ACB o BCA. Para las combinaciones esos tres elementos forman un solo grupo. En cambio, en las variaciones se considerarían tres grupos distintos.
Un ejemplo para diferenciar combinaciones y variaciones es la selección de personas:
- Si se desea elegir a tres personas de un grupo para viajar a una conferencia no importa el orden de elección de éstas en el grupo. En este caso se calcula mediante combinaciones.
- Si en cambio se desea elegir a tres personas de un grupo para ocupar tres cargos en una empresa (gerente, subgerente y secretario) sí importa el orden.
Ejemplo:
María-gerente
David-subgerente
Rocío-secretaria
Es distinto a que sean:
David-gerente
Rocío-subgerente
María-secretaria
Por lo tanto, se utilizan variaciones para calcular todas las posibilidades de elección.
La notación para las variaciones es:![]()
Fórmula: ![]()
EJEMPLO:
Formar las variaciones ternarias de los cuatro elementos A, B, C y D.
Se reemplazan los datos en la fórmula: m=4; n=3
![]()
Los grupos serían: ABC,ACB, BAC, BCA, CAB, CBA, ABD, ADB, BAD, BDA, DAB, DBA, ACD,ADC, CAD, CDA, DAC,DCA, BCD, BDC, CDB,CBD,DBC, DCB.
Permutaciones (ordinarias)
Es un caso particular de las variaciones en donde pueden intervenir todos los elementos. Se consideran distintos grupos cuando el orden de los elementos difiere.
La notación para las permutaciones es:![]() , siendo n=m.
, siendo n=m.
![]()
EJEMPLO:
¿Cuántas permutaciones pueden hacerse con las letras de la palabra MÉXICO?
Las letras de la palabra México son 6, por lo tanto n=6.
![]()

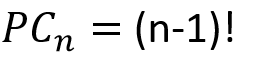
Para seguir estudiando más contenidos de combinatoria puedes ingresar a la Enciclopedia de Matemática Secundaria, tomo 2, capítulo 2.
A PRACTICAR LO APRENDIDO
COMBINACIONES
- Calcular el número de combinaciones de 8 objetos tomados de cinco en cinco.
- ¿Cuántos grupos diferentes de ocho cartas se pueden dar con una baraja de 40 cartas?
VARIACIONES
- ¿De cuantas maneras se pueden cubrir tres cargos directivos en un club deportivo si hay 10 postulantes?
- ¿De cuántas formas se pueden sentar 4 personas en 6 asientos?
PERMUTACIONES
- ¿De cuántas formas posibles se pueden ordenar 10 libros en un estante?
- ¿De cuántas maneras se pueden intercambiar las gomas de un automóvil, incluyendo la de repuesto?
RESPUESTAS
COMBINACIONES
- 56 maneras.
- 76.904.685 formas.
VARIACIONES
- 720 maneras.
- 360 formas.
PERMUTACIONES
- 3.628.800 formas.
- 120 maneras.




 VOLVER A LOS ARTÍCULOS
VOLVER A LOS ARTÍCULOS