CAPÍTULO 3 / TEMA 5

Problemas con fracciones

La fracciones están presentes en la vida cotidiana. Su utilidad es inmensa y sin ellas muchos cálculos matemáticos serían más complejos. La resolución de operaciones como la suma, la resta, la división y la multiplicación se lleva a cabo de una manera particular cuando involucran fracciones.

Cálculo de fracciones equivalentes

Las fracciones equivalentes son aquellas que representan la misma cantidad pero sus numeradores y denominadores no son iguales. Se pueden calcular por amplificación o por simplificación:

Para encontrar una fracción equivalente por amplificación tenemos que multiplicar el numerador y denominador por un mismo número. En este caso, las fracciones \frac{1}{2} y \frac{2}{4} son equivalentes porque:

Por otro lado, para calcular una fracción equivalente por simplificación, debemos hacer el procedimiento contrario, es decir, dividir el numerador y denominador por un mismo número. En este caso, ambos términos de la fracción deben tener un divisor común, de lo contrario se dice que la fracción es irreducible.

Las fracciones \frac{10}{4} y \frac{5}{2} son fracciones equivalentes porque:

¿Sabías qué?
Las fracciones irreducibles son aquellas cuyo numerador y denominador no tienen un divisor común.

Adición y sustracción de fracciones homogéneas

Sumar o restar fracciones homogéneas es sencillo. Primero se suman o restan los numeradores según indique el signo y el número obtenido será el numerador de la fracción resultante, luego se coloca el mismo denominador. Por ejemplo:

Calcula: 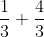\frac{1}{3}+\frac{4}{3}

Suma los dos numeradores, que son 1 y 4, y luego coloca el mismo denominador de las fracciones. La fracción resultante es entonces \frac{5}{3}.

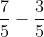
Calcula: \frac{7}{5}-\frac{3}{5}

Resta los numeradores, 7 y 3, y el número obtenido será el numerador de la fracción resultante cuyo denominador será el mismo de las fracciones originales. En este caso, el resultado es \frac{4}{5}.

En la práctica simplificamos fracciones hasta su mínima expresión, es decir, obtenemos fracciones equivalentes que no tengan divisores comunes entre su numerador y su denominador. Hacemos esto porque dichas fracciones simplifican la escritura y los cálculos. Por lo general, para reducir fracciones empleamos los criterios de la divisibilidad.

VER INFOGRAFÍA

Adición y sustracción de fracciones heterogéneas

Las fracciones heterogéneas son aquellas que tienen distinto denominador. Un método para resolver adiciones y sustracciones de este tipo de fracciones es el método en cruz, el cual consiste en calcular fracciones equivalentes con el mismo denominador y luego sumar o restar según indique el signo.

Pasos para resolver sumas y restas de fracciones heterogéneas

  1. Multiplica el numerador de la primera fracción por el denominador de la segunda fracción, luego coloca el signo según indique la operación y seguido de eso multiplica el denominador de la primera fracción por el numerador de la segunda. La suma o resta de esos dos productos será el numerador de la fracción resultante.
  2. Multiplica el denominador de la primera fracción por el denominador de la segunda, el resultado de esa multiplicación será el denominador de la fracción resultante.

Calcula: 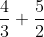\frac{4}{3}+\frac{5}{2}

Se aplican los pasos anteriores, es decir: multiplicamos el numerador de la primera fracción (4) por el denominador de la segunda (2), colocamos el signo más (+) y luego multiplicamos el denominador de la primera fracción (3) por el numerador de la segunda fracción (5). Ambos productos forman parte del numerador de la fracción resultante.

Luego multiplicamos los denominadores y el producto formará parte del denominador de la fracción resultante.

Resolvemos los productos.

Finalmente, resolvemos la suma en el denominador y obtenemos el resultado:

 

Calcula: 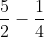\frac{5}{2}-\frac{1}{4}

El procedimiento es el mismo que el anterior, pero al momento de realizar los productos cruzados colocamos el signo menos (−) y luego restamos. El procedimiento sería el siguiente:

Simplificación

Podemos simplificar la fracción \frac{18}{8} y llevarla a su mínima expresión, para esto solo dividimos el numerador y el denominador por dos (2). Por lo tanto:

\frac{18}{8}=\frac{9}{4}

Multiplicación de fracciones

La multiplicación de fracciones se realiza de forma lineal entre sus elementos, es decir, primero multiplicamos todos los numeradores y el producto será el numerador resultante. Luego multiplicamos todos los denominadores y el producto será el denominador de la fracción resultante.

Calcular: \frac{5}{3}\times \frac{3}{2}.

Simplificación

Podemos simplificar la fracción \frac{15}{6} y llevarla a su mínima expresión, para esto solo dividimos el numerador y el denominador por tres (3). Por lo tanto:

\frac{15}{6}=\frac{5}{2}

La inversa de una fracción es aquella en la que su numerador es igual al denominador y el denominador es igual al numerador de la primera fracción en ambos casos. La inversa de la fracción 3/2 es 2/3 y la inversa de 5/8 es 8/5. Si multiplicamos una fracción por su inversa, el resultado siempre va a ser la unidad. En este sentido 3/2 x 2/3 = 1 y 5/8 x 8/5 = 1.
¡A practicar!

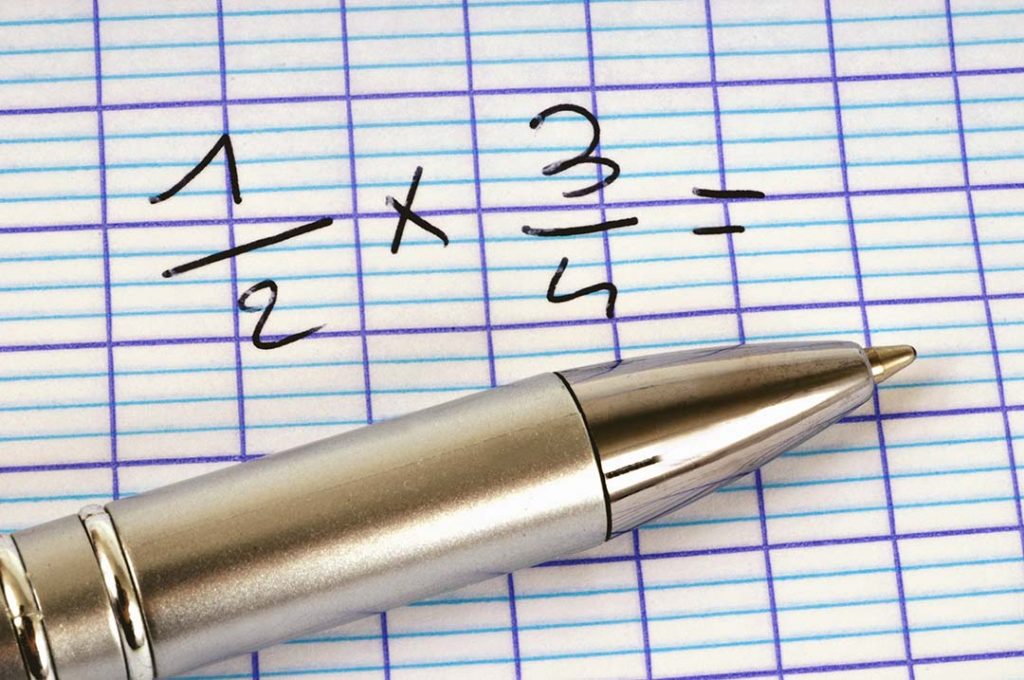
1. Resuelve las siguientes adiciones y sustracciones de fracciones:

a) \frac{7}{9}+\frac{1}{9}

Solución
\frac{8}{9}

b) \frac{3}{5}-\frac{1}{2}

Solución
\frac{1}{10}

c) \frac{9}{7}+\frac{5}{7}

Solución
\frac{14}{7}

La fracción simplificada es \frac{2}{1}=2

d) \frac{13}{20}-\frac{8}{20}

Solución
\frac{5}{20}

La fracción simplificada es \frac{1}{4}. 

e) \frac{4}{5}+\frac{6}{9}

Solución
\frac{66}{45}

La fracción simplificada es \frac{22}{15}.

2. Resuelve las siguientes multiplicaciones:

a) \frac{3}{5}\times \frac{4}{9}

Solución
\frac{12}{45}

La fracción simplificada es \frac{4}{15}. 

b) \frac{5}{8}\times \frac{3}{9}

Solución
\frac{15}{72}

La fracción simplificada es \frac{5}{24}.

c) \frac{1}{8}\times \frac{7}{2}

Solución
\frac{7}{16}

d) \frac{3}{8}\times \frac{4}{7}

Solución
\frac{12}{56}

La fracción simplificada es \frac{3}{14}.

e) \frac{9}{4}\times \frac{8}{3}

Solución
\frac{72}{12}

La fracción equivalente es \frac{6}{1}=6

RECURSOS PARA DOCENTES

Artículo “Adición y sustracción de fracciones”

En este artículo destacado se exponen diferentes formas de resolver adiciones y sustracciones de fracciones con igual o diferente denominador.

VER

Artículo “Multiplicación y división de fracciones”

En este artículo se expone cómo resolver problemas de multiplicación de fracciones. También describe como realizar la simplificación de estos números y ayuda a comenzar a trabajar con problemas de división de fracciones.

VER