Tag: propiedades de la suma

CAPÍTULO 2 / TEMA 2

ADICIÓN O SUMA

SI TIENES 2 CARAMELOS Y LUEGO TE REGALAN 2 CARAMELOS MÁS, ¿CUÁNTOS CARAMELOS TIENES? ESTE ES UN PROBLEMA QUE SE RESUELVE POR MEDIO DE UNA SUMA. LA SUMA O ADICIÓN ES UNA OPERACIÓN EN LA QUE AGREGAMOS O AGRUPAMOS CANTIDADES PARA OBTENER UN RESULTADO FINAL. LOS NÚMEROS A SUMAR SE LLAMAN SUMANDOS Y EL TOTAL SE LLAMA SUMA.

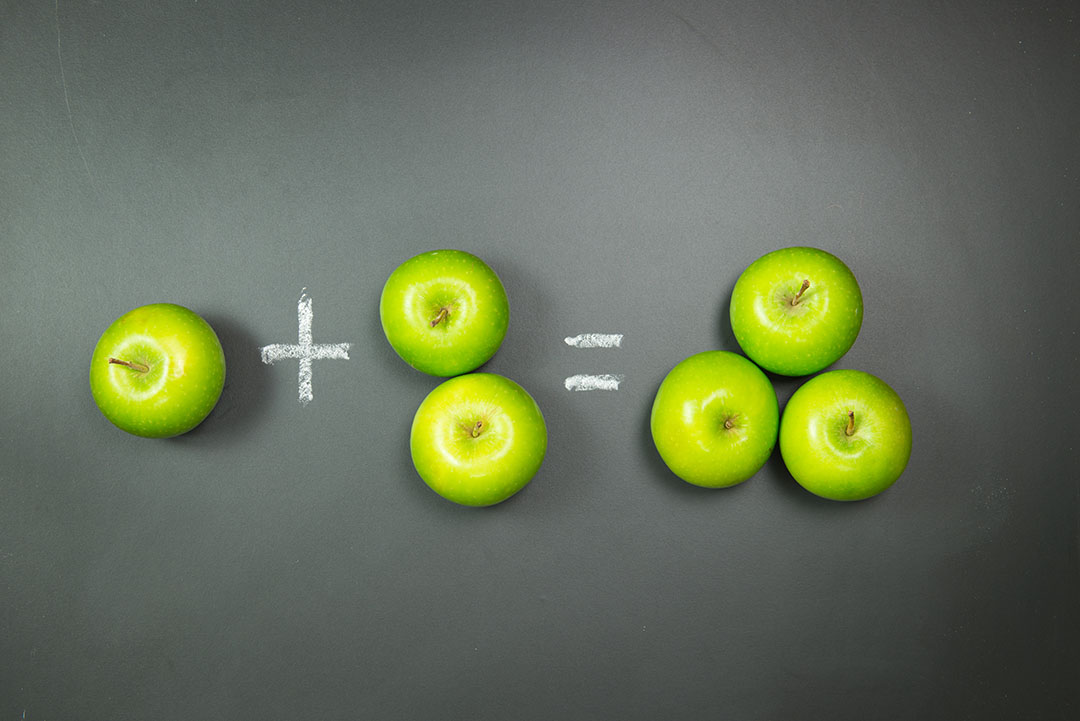
PUEDES RESOLVER UNA SUMA A TRAVÉS DE UN CÁLCULO MENTAL, UN GRÁFICO, UNA CUENTA HORIZONTAL O VERTICAL. LA SUMA ES UNA OPERACIÓN EN LA QUE AGRUPAMOS CANTIDADES LLAMADAS SUMANDOS Y EL RESULTADO SE DENOMINA SUMA. EN ESTA IMAGEN VEMOS UNA SUMA DE MANZANAS EN LA QUE SE AGRUPAN 1 MANZANA CON OTRAS 2 MANZANAS PARA TENER UN TOTAL DE 3 MANZANAS.

LA SUMA Y SUS ELEMENTOS

ANA Y NICO DECIDIERON LLEVAR SUS OSITOS PARA JUGAR EN EL RECREO DE LA ESCUELA. ¿CUÁNTOS OSITOS TIENEN ENTRE LOS DOS?

  • 1 Y 2 SON LOS SUMANDOS.
  • 3 ES LA SUMA O EL RESULTADO.

¡VAMOS A SUMAR!

ESCRIBE LOS SUMANDOS Y LA SUMA EN CADA CASO.

SOLUCIÓN

SOLUCIÓN
 

PROPIEDADES DE LA SUMA

PROPIEDAD CONMUTATIVA

ESTA PROPIEDAD EXPLICA QUE EL ORDEN DE LOS SUMANDO NO ALTERA LA SUMA O RESULTADO.

 

PROPIEDAD ASOCIATIVA

ESTA PROPIEDAD EXPLICA QUE SI SUMAMOS TRES NÚMEROS, PODEMOS AGRUPAR DOS Y LUEGO SUMAR EL TERCERO.

ELEMENTO NEUTRO: OTRA PROPIEDAD A CONOCER

ESTA PROPIEDAD NOS INDICA QUE LA SUMA DE TODO NÚMERO MÁS EL CERO ES IGUAL AL MISMO NÚMERO, DE MANERA QUE EL CERO ES EL ELEMENTO NEUTRO DE LA SUMA.

APLICACIÓN DE LA SUMA

A VECES NECESITAMOS SUMAR NÚMEROS MÁS GRANDES, ENTONCES NO PODEMOS DIBUJAR CADA ELEMENTO Y CONTARLO PORQUE NOS LLEVARÍA MUCHO TIEMPO. ¡APRENDERÁS AHORA OTRA FORMA DE SUMAR!

PRIMERO COLOCAMOS LOS SUMANDOS UNOS SOBRE OTRO. ESCRIBIMOS LAS UNIDADES EN LA COLUMNA DE LAS UNIDADES Y LAS DECENAS EN LA COLUMNA DE LAS DECENAS.

LUEGO SUMAMOS LAS UNIDADES: 1 + 6 = 7.

DESPUÉS SUMAMOS LAS DECENAS: 1 + 1 = 2.

PUEDES ESCRIBIR ESTA SUMA DE FORMA HORIZONTAL:

11 + 16 = 27

¡ES TU TURNO!

REALIZA ESTAS SUMAS:

  • 14 + 11
  • 23 + 35
  • 29 + 10
  • 44 + 31
  • 25 + 33
  • 18 + 61
SOLUCIÓN

LOS CÁLCULOS MENTALES SON AQUELLOS QUE PUEDES REALIZAR MENTALMENTE, SIN NECESIDAD DE EMPLEAR UNA CALCULADORA NI REALIZAR ANOTACIONES. LOS CÁLCULOS MENTALES TE PERMITEN ALCANZAR UNA MAYOR RAPIDEZ MENTAL, DISPONER DE MÁS RECURSOS PARA RESOLVER PROBLEMAS Y TAMBIÉN AUMENTAR TU CAPACIDAD DE ATENCIÓN Y CONCENTRACIÓN. ¡INTENTA HACER UNA SUMA MENTAL!
¿SABÍAS QUÉ?
PARA RESOLVER CÁLCULOS MENTALMENTE PUEDES UTILIZAR OTROS QUE YA SEPAS DE MEMORIA O HAYAS REALIZADO ANTES.

SITUACIONES PROBLEMÁTICAS

1. ES EL CUMPLEAÑOS DE MARTA. SU TÍA LE REGALÓ $ 15 Y SU ABUELO LE REGALÓ $ 23. ¿CUÁNTO DINERO LE REGALARON A MARTA?

  • DATOS

DINERO REGALADO POR SU TÍA: $ 15

DINERO REGALADO POR SU ABUELO: $ 23

  • REFLEXIONA

PARA CONOCER LA CANTIDAD DE DINERO QUE LE REGALARON EN TOTAL TENEMOS QUE SUMAR LAS DOS CANTIDADES. PARA ESO COLOCAMOS LOS SUMANDO UNO SOBRE OTRO. LUEGO SUMAMOS LAS UNIDADES Y DESPUÉS LAS DECENAS.

  • CALCULA

  • RESPUESTA

A MARTA LE REGALARON $ 38.

2. LA MAMÁ DE JULIETA COMPRÓ 20 GLOBOS ROJOS Y 25 GLOBOS NARANJAS PARA DECORAR EL SALÓN EL DÍA DE SU CUMPLEAÑOS ¿CUÁNTOS GLOBOS COMPRÓ EN TOTAL?

  • DATOS

GLOBOS ROJOS: 20

GLOBOS NARANJAS: 25

  • REFLEXIONA

PARA CONOCER LA CANTIDAD DE GLOBOS COMPRADOS TENEMOS QUE SUMAR LAS DOS CANTIDADES. PARA ESO COLOCAMOS LOS SUMANDO UNO SOBRE OTRO. LUEGO SUMAMOS LAS UNIDADES Y DESPUÉS LAS DECENAS.

  • CALCULA

  • RESPUESTA

LA MAMÁ DE JULIETA COMPRÓ EN TOTAL 45 GLOBOS.

3. CARLOS INVITÓ A SU FESTEJO DE CUMPLEAÑOS A 14 NIÑOS Y 21 NIÑAS ¿CUÁNTOS INVITADOS HAY EN TOTAL?

  • DATOS

NIÑOS INVITADOS: 14

NIÑAS INVITADAS: 21

  • REFLEXIONA

PARA CONOCER LA CANTIDAD NIÑOS INVITADOS EN TOTAL TENEMOS QUE SUMAR LAS DOS CANTIDADES. PARA ESO COLOCAMOS LOS SUMANDOS UNO SOBRE OTRO. LUEGO SUMAMOS LAS UNIDADES Y DESPUÉS LAS DECENAS.

  • CALCULA

  • RESPUESTA

CARLOS INVITÓ A 35 NIÑOS EN TOTAL.

¡A PRACTICAR!

RESUELVE ESTAS SUMAS.

  • 28 + 11
SOLUCIÓN
28 + 11 = 39
  • 36 + 52
SOLUCIÓN
36 + 52 = 88
  • 15 + 33
SOLUCIÓN
15 + 33 = 48
  • 78 + 10
SOLUCIÓN
78 + 10 = 88
  • 24 + 25
SOLUCIÓN
24 + 25 = 49
  • 16 + 62
SOLUCIÓN
16 + 62 = 78
RECURSOS PARA DOCENTES

Artículo “Propiedades de la suma”

Con este recurso podrás ampliar la información sobre las propiedades de las sumas.

VER

CAPÍTULO 2 / TEMA 1

ADICIÓN

La adición o suma es una de las operaciones básicas de las matemáticas. La usamos casi todos los días y gracias a ella sabemos cuántos alumnos hay en una escuela, cuántas pelotas hay en la cancha o cuántos libros tenemos. Como verás, sumar números de 4 cifras implica un orden y podemos hacerlo de acuerdo a sus propiedades.

La adición es una operación matemática que nos permite agregar o reunir dos o más cantidades en un mismo número. Los términos de la adición son los sumandos y suma. Las cantidades que se suman son los sumandos y el resultado es la suma. Cuando los números son pequeños podemos hacer sumas con los dedos y escribirlo de forma horizontal.

la adición y sus elementos

La adición es una operación que consiste en añadir una cantidad a otra. Los términos de la adición son los sumandos y  la suma.

¿CÓMO resolver una adición?

Si un número tiene más de tres cifras conviene usar el algoritmo de la suma. Esto consiste en ordenar los sumandos de tal manera que las unidades, las decenas, las centenas y las unidades de mil están en las mismas columnas. Luego sumamos cada posición desde la derecha. Los pasos son los siguientes:

1. Sumamos las unidades: 8 + 1 = 9.

2. Sumamos las decenas: 7 + 2 = 9.

 

3. Sumamos las centenas: 4 + 3 = 7.

 

4. Sumamos las unidades de mil: 3 + 3 = 6.

– Otros ejemplos:

 

¡Es tu turno!

Realiza esta sumas:

  • 8.605 + 1.382
  • 5.074 + 4.523
  • 1.841 + 7.106
Solución

 

Equivalencia de interés

  • 1 unidad de mil = 1.000 unidades
  • 1 centena = 100 unidades
  • 1 decena = 10 unidades
  • 1 unidad = 1 unidad

¿Sabías qué?
La operación opuesta a la adición es la sustracción o resta.
Cuando colocamos los sumandos uno sobre otro y hacemos coincidir las posiciones, empleamos el algoritmo de la suma. En este proceso sumamos primero las unidades, luego las decenas, las centenas y finalmente las unidades de mil. Cuando un resultado es mayor a 9, se coloca la decena en la columna de la izquierda y se reagrupan las cifras.

¿cómo resolver una adición con llevadas?

Las adiciones o sumas con llevadas las podemos resolver de la misma manera que las adiciones anteriores, la única diferencia es que debemos reagrupar las decenas, centenas o unidades de mil cuando una de las sumas de las posiciones sea superior a 9. Para sumas de números de cuatro cifras los pasos son estos:

1. Sumamos las unidades: 2 + 5 = 7.

 

2. Sumamos las decenas: 3 + 6 = 9.

 

3. Sumamos las centenas: 6 + 6 = 12. Como el resultado es mayor a 9 colocamos la unidad (2) en la casilla debajo de la suma de centenas y el 1 lo colocamos en la columna de las unidades de mil.

4. Sumamos las unidades de mil y consideramos el 1 agregado antes: 1 + 2 + 3 = 6.

 

– Otros ejemplos:

 

¿Sabías qué?
En una adición o suma podemos hacer llevadas en una o más cifras.
La adición está presente en muchas situaciones de la vida diaria. Si observas a tu alrededor, hay muchas cosas en las que podemos utilizar esta operación. Uno de los casos más frecuentes es cuando compramos productos en el supermercado. Allí debemos sumar todos los precios de cada artículo para pagar un total. Las máquinas registradoras hacen este cálculo rápidamente.

 

propiedades de la adición

La adición tiene algunas propiedades que la caracterizan. Estas son: la propiedad conmutativa, la propiedad asociativa y el elemento neutro.

Propiedad conmutativa

Al invertir o cambiar de lugar los sumandos el resultado es el mismo, es decir, el orden de los sumandos no altera la suma obtenida.

Propiedad asociativa

Sin importar la agrupación de los términos el resultado será el mismo.

Elemento neutro

La suma de todo número más cero es igual al mismo número, de manera que 0 es el elemento neutro de la suma.

1.568 + 0 = 1.568

 

El ábaco es un instrumento que sirve para efectuar operaciones matemáticas sencillas. Este es un cuadro de madera con barras paralelas por las que corren bolas movibles. El ábaco no solo nos ayuda a sumar y restar con mayor fluidez, sino que además podemos resolver operaciones más complejas como la multiplicación y la división.

 

¡A practicar!

1. Resuelve las siguientes adiciones:

  • 5.328 + 2.419
Solución

  • 3.686 + 5.607
Solución

  • 4.368 + 5.177
Solución

  • 8.645 + 480
Solución

  • 5.502 + 3.199
Solución

  • 6.098 + 2.174
Solución

 

2. Resuelve estas adiciones y aplica la propiedad conmutativa:

  • 560 + 199
Solución

560 + 199 = 759

199 + 560 = 759

  • 1.795 + 528
Solución

1.795 + 528 = 2.323

528 + 1.795 = 2.323

  • 237 + 797
Solución

237 + 797 = 1.034

797 + 237 = 1.034

  • 1.300 + 788
Solución

1.300 + 788 = 2.088

788 + 1.300 = 2.088

 

3. Realiza la siguientes sumas y aplica la propiedad distributiva.

  • 150 + 430 + 670
Solución

(150 + 430) + 670 = 580 + 670 = 1.250

150 + (430 + 670) = 150 + 1.100 = 1.250

  • 720 + 340 + 480
Solución

(720 + 340) + 480 = 1.060 + 480 = 1.540

720 + (340 + 480) = 720 + 820 = 1.540

  • 500 + 200 + 400
Solución

(500 + 200) + 400 = 700 + 400 = 1.100

500 + (200 + 400) = 500 + 600 = 1.100

  • 6.000 + 500 + 1.000
Solución

(6.000 + 500) + 1.000 = 6.500 + 1.000 = 7.500

6.000 + (500 + 1.000) = 6.000 + 1.500 = 7.500

 

RECURSOS PARA DOCENTES

Artículo “Cómo enseñar a sumar y a restar”

El siguiente material le brindará orientaciones generales para enseñar a sus alumnos a sumar y a restar.

VER

Artículo “Propiedades de la suma”

Con este recurso se podrá ampliar la información referida a las propiedades de la adición.

VER

Artículo “Suma con tres sumandos”

Este artículo explica paso a paso cómo realizar cálculos con tres sumandos.

VER