Sistemas de referencia
Son convencionalismos adoptados por el ser humano para medir la posición y otras magnitudes físicas. Se usan para hallar cuerpos celestes en el espacio y son la base para determinar nuestra ubicación en el planeta. También permiten establecer comparaciones y transformaciones entre las figuras representadas.
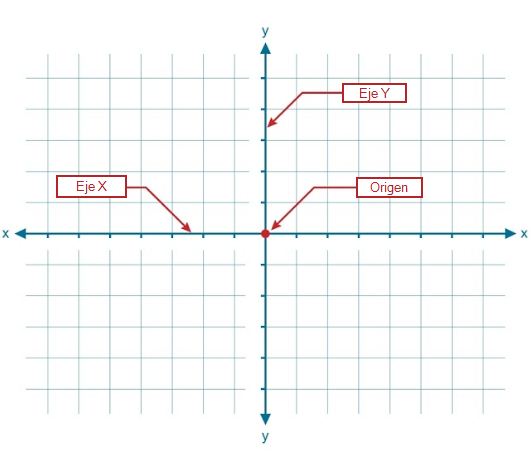
Ejes de coordenadas
El sistema de coordenadas cartesianas es uno de los sistemas de referencias usados para ubicar puntos en el espacio. En este caso específicamente se explicarán estas coordenadas orientadas al plano, es decir, en dos dimensiones.
El plano donde ubicamos los puntos se denomina plano cartesiano y está formado por los siguientes elementos:
- Eje X: es también denominado eje de las abscisas, y se encuentra ubicado dentro del plano en forma horizontal.
- Eje Y: es conocido también como eje de las ordenadas y está ubicado en sentido vertical dentro del plano.
- Origen: es el punto de intersección entre los ejes de coordenadas X e Y.
¿Cómo graficar un punto en el plano cartesiano?
Un punto está definido por un par de números que hacen referencia a su posición respecto al eje X y al eje Y. Estos puntos son denominados coordenadas cartesianas y permiten graficarlo.
Para hacerlo, dividimos los ejes en segmentos con la misma longitud y a cada uno le asignamos el valor de un número entero. A la derecha del origen, escribimos los números de menor a mayor, esos serán los valores del eje X. Arriba del origen escribimos los números que le siguen al cero de menor a mayor, esos serán los valores del eje Y:

Para ubicar un punto en el plano necesitamos las coordenadas de cada eje, que de ahora en adelante llamaremos coordenada en X y coordenada en Y para hacer mención a cuál eje se refieren. La coordenada X determina cuán a la derecha del origen está ubicado el punto; mientras que la coordenada Y, cuán arriba del origen está el punto.
La manera más frecuente de representar un punto es a través de paréntesis, y dentro indicamos la coordenada X y la coordenada Y, separadas por una coma:
El punto desde dónde se empieza a contar es en el origen porque se encuentra en la coordenada (0,0) lo que quiere decir que está a 0 posiciones de la derecha y a 0 posiciones hacia arriba.
Por ejemplo:
El punto A (3,2) se encuentra a tres posiciones a la derecha y a dos posiciones hacia arriba. Si lo queremos graficar, cada coordenada debe estar representada en el respectivo eje y el punto de intersección de ambas sería el punto A:

Cuando algunas de las coordenadas del punto sea igual a cero, significa que el punto se encuentra sobre el eje al cual corresponde la coordenada diferente de cero. Por ejemplo, el punto B (0,3) indica que se movió cero posiciones a la derecha y tres posiciones hacia arriba, por lo tanto se ubica sobre el eje Y que es el que tiene la coordenada diferente de cero:

Ejes de simetrías
La simetría es una relación proporcionada entre las partes que componen un todo. Así, por ejemplo, decimos que una imagen es simétrica cuando su forma no cambia si es girada o volteada. Para que exista simetría entre dos objetos, ambos deben ser del mismo tamaño y de la misma forma y uno debe estar en una orientación diferente a la del primero.

El eje de simetría es una línea imaginaria que divide al dibujo en dos partes idénticas pero con diferente orientación. Los ejes de simetría pueden ser horizontales, verticales o inclinados.

De acuerdo a la figura geométrica, algunas pueden presentar uno o más ejes de simetría. Otras, en cambio, no presentan ninguno. Cuando una figura no es simétrica se denomina asimétrica.

Por ejemplo, no todos los triángulos tienen ejes de simetría, todo depende de su tipo. Si son equiláteros tienen tres ejes de simetría; si son isósceles tienen dos ejes de simetría, y si son escalenos no tienen ningún eje de simetría.

Transformaciones isométricas
Las transformaciones isométricas son los cambios de posición u orientación que experimenta una figura sin alterar su forma.
Traslación
Es un tipo de transformación isométrica donde se mueven todos los puntos de una figura en una misma dirección, sentido y longitud.

Rotación
También es conocida como giro. Es una transformación isométrica en la que la figura se mueve alrededor de un punto sin alterar su forma. El movimiento es determinado por un ángulo de rotación y puede ser en sentido de las agujas del reloj o en sentido contrario.

La simetría entre dos objetos es un tipo de transformación isométrica porque a cada punto del objeto o figura se lo asocia a otro conocido como imagen. Cada punto está a una misma distancia del otro respecto al eje de simetría. Este tipo de transformación también se conoce como reflexión.

¡A practicar!
1. ¿Cuál es la posición de estos números?
a) 
b) 
c) 
d) 
e) 
2. ¿A cuál de los siguientes puntos corresponde la coordenada (6,3)?

3. ¿Cuál de estas figuras no es simétrica?
a) 
b)
c)
d)
4. ¿A qué tipo de transformación isométrica corresponde la gráfica?

 Corresponde al punto K (6,3).
Corresponde al punto K (6,3).