CAPÍTULO 6 / TEMA 1

REPRESENTACIÓN GRÁFICA DE DATOS

Habrás observado que muchas veces la información en los medios de comunicación está acompañada por una variedad de gráficos. Los gráficos son representaciones visuales de un conjunto de datos; por ejemplo, la cantidad de habitantes de cada ciudad del país o el porcentaje del crecimiento interanual de una economía. Son muy efectivos para mostrar relaciones entre diferentes valores y permiten comprender fácilmente distintas situaciones de la realidad.

Es frecuente encontrar gráficos en los análisis estadísticos que refuercen de forma visual la información necesaria. Estas representaciones se adaptan en cada caso a aquello que se busca transmitir y al objetivo de la investigación. Dichos resultados se presentan de forma rápida, directa, atractiva y comprensible para un conjunto amplio de personas.

LOS DATOS Y LAS GRÁFICAS

Un dato no es más que una información que permite describir alguna característica de una situación de estudio. Este puede ser un número, una palabra o cualquier símbolo. Si un dato describe una cualidad se dice que es cualitativo, pero si señala una cantidad se llama cuantitativo. Por ejemplo:

Datos cualitativos

Datos cuantitativos

– Profesión: {médico, policía, ingeniero}

– Color de ojos: {negro, azul, verde, marrón}

– Estado civil: {soltero, casado, viudo}

– Edad: {10 años, 11 años, 13 años}

– Peso: {40 kg, 37 kg, 41 kg}

– Cantidad de hermanos: {1, 3, 4}

Cuando tenemos una cantidad numerosa de datos recurrimos a las tablas. Allí, organizamos en filas y columnas los valores obtenidos y luego los clasificamos de acuerdo a los objetivos de la investigación. Posteriormente graficamos la información, pues estas gráficas brindan una mayor rapidez en la comprensión de los datos porque los presentan de forma clara, organizada y llamativa.

– Ejemplo:

30 personas fueron encuestadas acerca de cuál era su fruta favorita. Las respuestas obtenidas fueron las siguientes:

Manzana	Pera	Ananá	Ananá	Naranja	Naranja
Banana	Fresa	Naranja	Manzana	Naranja	Manzana
Naranja	Durazno	Manzana	Ananá	Naranja	Pera
Banana	Fresa	Banana	Fresa	Manzana	Fresa
Ananá	Naranja	Manzana	Ananá	Naranja	Banana

Con estos datos podemos realizar una tabla que muestre la frecuencia o al cantidad de veces que cada fruta se repite.

Fruta	Frecuencia
Manzana	6
Banana	4
Naranja	8
Pera	2
Ananá	5
Fresa	4
Durazno	1
Total	30

Si bien los datos se ven claramente en esta tabla, podemos graficarlos para que sea aún más sencillo visualizar cuáles son las frutas más o menos preferidas por este grupo de personas.

Elementos de los gráficos

Existen diferentes tipos de gráficos y la selección dependerá de la información que se quiera mostrar, sin embargo todos los gráficos tienen algunos elementos en común:

Título: todo gráfico debe tener un título para saber rápidamente de qué se trata. El mismo se ubica en la parte superior de la gráfica, debe ser claro, breve e informar sobre el contenido del cuadro.
Cuerpo: el cuerpo varía en función al estilo de gráfico que se seleccione, entre los más usados se encuentran el lineal, el de barras y el circular.

VER INFOGRAFÍA

TIPOS DE GRÁFICOS

Gráficos de barras

En este tipo de gráficos se construyen barras cuyas longitudes permiten comparar las categorías, observar los diferentes valores y obtener información con respecto a lapsos de tiempo. Las variables estudiadas se colocan en el eje horizontal y las frecuencias se colocan en el eje vertical, luego ubicamos los puntos y trazamos barras verticales para cada variable.

– Ejemplo:

Esta gráfica muestra la cantidad de hombres y mujeres en cada grado de un colegio.

Con esta gráfica vemos de forma muy clara la cantidad de hombres y mujeres que hay en cada grado. Nota que las barras de colores azul corresponden a los hombres y las barras de color naranja corresponden a las mujeres.

De acuerdo a la tabla, el grado con mayor cantidad de hombres es 6º (20), y el grado con menor cantidad de hombres es 1º (9).

¡Es tu turno!

Realiza la tabla de datos de acuerdo a la gráfica anterior.

Solución

Grado	Hombres	Mujeres	Total
1º	9	11	20
2º	10	15	25
3º	14	14	28
4º	15	17	32
5º	14	10	24
6º	20	11	31
7º	18	15	33
Total	100	93	193

¿Sabías qué?

Los gráficos de barras pueden ser verticales, horizontales, agrupados o apilados.

Gráficos lineales

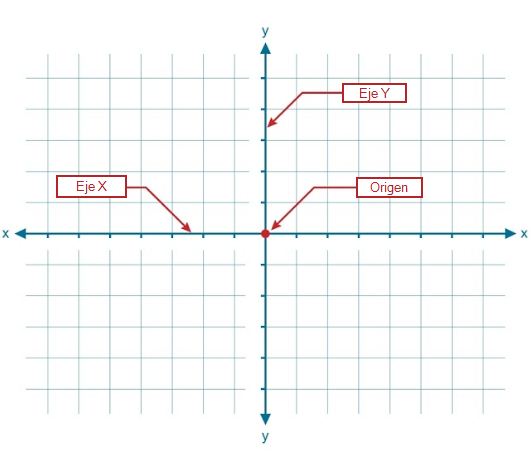
Los gráficos lineales, también llamados gráficos poligonales, se representan en un plano (dos dimensiones) mediante el uso de un sistema de coordenadas. Para construirlos basta con ubicar los puntos en el plano y luego unirlos por medio de líneas.

– Ejemplo:

Con los mismos datos del ejemplo anterior en el que realizamos un gráfico de barras podemos dibujar un gráfico lineal.

Gráficos circulares

También son conocidos como gráficos de torta o pastel. Se usan para comparar porcentajes con respecto a un total de datos. Son útiles cuando deseas mostrar una sola serie de datos, por ejemplo, el sexo de la población. Para hallar los porcentajes parciales se dividen los 360° del círculo de acuerdo a los valores dados.

– Ejemplo:

La siguiente tabla muestra la cantidad de huéspedes en un hotel según su nacionalidad:

Nacionalidad	Cantidad de turistas
Colombiana	12
Argentina	23
Chilena	5
Venezolana	15
Italiana	18
Total	73

Es normal colocar los valores de porcentajes en los gráficos de este tipo, para calcularlos solo dividimos la cantidad de cada nacionalidad entre el total de turista. Luego multiplicamos por 100. La suma de todos los porcentajes debe ser igual a 100 %.

Nacionalidad	Cantidad de turistas	Porcentaje
Colombiana	12	(12/73) × 100 = 16,44 %
Argentina	23	(23/73) × 100 = 31,50 %
Chilena	5	(5/73) × 100 = 6,85 %
Venezolana	15	(15/73) × 100 = 20,55 %
Italiana	18	(18/73) × 100 = 24,66 %
Total	73	100 %

Ahora, para ilustrar los datos en un círculo multiplicamos la fracción de cada nacionalidad por 360°. La suma de todos los grados debe ser igual a 360°. Por conveniencia redondeamos a la unidad cada producto.

Nacionalidad	Cantidad de turistas	Grados
Colombiana	12	(12/73) × 360° = 59,18° ≈ 59°
Argentina	23	(23/73) × 360° = 113,42° ≈ 113°
Chilena	5	(5/73) × 360° = 24,66° ≈ 25°
Venezolana	15	(15/73) × 360° = 73,97° ≈ 74°
Italiana	18	(18/73) × 360° = 88,77° ≈ 89°
Total	73	360°

De ese modo, tras dibujar la circunferencia, medimos con el transportador los grados correspondientes a cada porción y anotamos el porcentaje redondeado que lo representa.

¿Qué es una muestra?

Se denomina población al conjunto de elementos estudiados, es decir, al total. Una muestra es una parte de esa población, es decir, es una porción seleccionada que resulta representativa del conjunto. Se toman muestras cuando la población que se quiere estudiar es muy amplia e inabarcable, entonces se decide realizar una selección estratégica que recorte la cantidad de individuos a estudiar y que mantengan los rasgos representativos de toda la población analizada.

IMPORTANCIA DE REPRESENTAR DATOS EN GRÁFICOS

La estadística, entre otras cosas, se encarga de recopilar, analizar y sistematizar datos. Luego, debe comunicar la información generada en este proceso. La presentación de datos es uno de los aspectos mayormente utilizados en la estadística descriptiva. Los gráficos son muy importantes ya que posibilitan un abordaje dinámico, claro y entretenido.

En este sentido, los gráficos son una gran herramienta ya que permiten:

Registrar datos de manera clara y concreta.
Comunicar la información en forma sencilla.
Comprender la estructura del conjunto de datos.

La cartografía tiene como objetivo la concepción, redacción y realización de los mapas, es decir, la representación plana y simplificada de toda o de una parte de la superficie terrestre. Los mapas estadísticos o cartogramas son aquellos que presentan datos por regiones o zonas. Al igual que en un mapa topográfico, los colores y las tramas indican áreas que están en el mismo rango de valores.

¡A practicar!

Observa los gráficos y responde:

1. Marta vendió magdalenas durante toda la semana. La cantidad de magdalenas vendidas se muestra en el siguiente gráfico:

¿Cuántas magdalenas vendió Marta el lunes?
Solución
Vendió 10 magdalenas.

¿Cuál día vendió más magdalenas?
Solución
El martes.

¿Cuál día vendió menos magdalenas?
Solución
El domingo.

¿Cuántas magdalenas vendió durante la semana?
Solución
Vendió 68 magdalenas durante la semana.

¿Cuál día vendió solo 8 magdalenas?
Solución
El viernes.

2. Se hizo una encuesta sobre el deporte favorito de un grupo de estudiantes. Los resultados se muestran en este gráfico.

¿Cuál es el deporte favorito de la mayoría de encuestados?
Solución
El fútbol.

¿Qué porcentaje de encuestados prefiere el béisbol?
Solución
El 14 %.

¿Qué porcentaje de encuestados prefiere el baloncesto?
Solución
El 23 %.

¿Cuál es el deporte menos preferido por los encuestados?
Solución
El béisbol.

RECURSOS PARA DOCENTES

Artículo “Gráficos estadísticos”

Con el siguiente artículo podrás ampliar tu conocimiento sobre tipos de gráficos estadísticos y sus funciones.

VER

Artículo “Lectura de gráficos”

En el siguiente artículo encontrarás ejemplos claros y explicados para abordar la interpretación y lectura de gráficos.

VER

CAPÍTULO 5 / TEMA 3

FRACCIONES Y SUS GRÁFICAS

CUANDO CONTAMOS NUESTROS JUGUETES O LÁPICES USAMOS LOS NÚMEROS NATURALES: 1, 2, 3, … PERO ¿QUÉ SUCEDE SI SOLO TENEMOS LA MITAD DE UN LÁPIZ? EN ESTOS CASOS USAMOS UN TIPO DE NÚMEROS LLAMADO FRACCIÓN. LAS FRACCIONES REPRESENTAN UNA PARTE DE UN ENTERO, ESTÁN FORMADAS POR DOS NÚMEROS NATURALES Y SON MÁS COMUNES DE LOS QUE CREES. ¡APRENDAMOS A GRAFICARLAS!

¿QUÉ ES UNA FRACCIÓN?

UNA FRACCIÓN REPRESENTA LA PARTE DE UN TODO O DE UNA UNIDAD DIVIDIDA EN PARTES IGUALES.

UNA NARANJA ENTERA ES IGUAL A UNA UNIDAD O EL “TODO”. OBSERVA LA IMAGEN, ¿LA NARANJA ESTÁ ENTERA? ¡NO! ESTÁ PICADA A LA MITAD Y HAY DOS MITADES. SI COMEMOS UNA DE ESTAS PARTES, DECIMOS QUE COMIMOS “MEDIA NARANJA”. ESTO ES UN EJEMPLO DE FRACCIÓN PORQUE COMIMOS UNA PARTE DE UN TODO. PIENSA: ¿EN QUÉ OTRA OCASIÓN USAMOS FRACCIONES?

VER INFOGRAFÍA

ELEMENTOS DE UNA FRACCIÓN

LA FRACCIÓN TIENE DOS ELEMENTOS SEPARADOS POR UNA RAYA: EL NÚMERO DE ARRIBA SE LLAMA NUMERADOR Y EL DE ABAJO SE LLAMA DENOMINADOR.

EL NUMERADOR ES IGUAL A LA CANTIDAD DE PARTES QUE SE HAN TOMADO DEL ENTERO.
EL DENOMINADOR ES IGUAL A LA CANTIDAD DE PARTES EN LAS QUE SE HA DIVIDIDO AL ENTERO.

TIPOS DE FRACCIONES

LAS FRACCIONES PUEDEN SER PROPIAS O IMPROPIAS.

LAS FRACCIONES PROPIAS TIENEN EL NUMERADOR MENOR AL DENOMINADOR.

POR EJEMPLO: $\frac{1}{2}$ , $\frac{3}{5}$ Y $\frac{8}{10}$ .

LAS FRACCIONES IMPROPIAS TIENEN EL NUMERADOR MAYOR AL DENOMINADOR.

POR EJEMPLO: $\frac{7}{5}$ , $\frac{10}{4}$ Y $\frac{5}{3}$ .

¿SABÍAS QUÉ?

LAS FRACCIONES TAMBIÉN SE PUEDEN EXPRESAR CON UNA DIAGONAL, POR EJEMPLO, $\frac{1}{2}$ ES IGUAL A 1/2.

¿CÓMO GRAFICAR FRACCIONES?

AL SER LAS PARTES DE UN TODO O UNIDAD, PODEMOS DIBUJAR FRACCIONES POR MEDIO DE GRÁFICOS CON FIGURAS GEOMÉTRICAS.

SI QUEREMOS GRAFICAR LA FRACCIÓN $\boldsymbol{\frac{1}{2}}$ LOS PASOS SON LOS SIGUIENTES:

1. DIBUJAMOS CUALQUIER FIGURA GEOMÉTRICA. EN ESTE CASO DIBUJAMOS UN RECTÁNGULO.

2. VEMOS EL DENOMINADOR DE LA FRACCIÓN. EL DENOMINADOR DE LA FRACCIÓN $\boldsymbol{\frac{1}{{\color{Red} 2}}}$ ES 2, ASÍ QUE DIVIDIMOS EL RECTÁNGULO EN 2 PARTES IGUALES.

3. VEMOS EL NUMERADOR DE LA FRACCIÓN. EL NUMERADOR DE LA FRACCIÓN $\boldsymbol{\frac{{\color{Red} 1}}{2}}$ ES 1, ASÍ QUE COLOREAMOS UNA SOLA PARTE DEL RECTÁNGULO.

– OTRO EJEMPLO:

GRAFIQUEMOS LA FRACCIÓN $\boldsymbol{\frac{3}{4}}$ .

PRIMERO DIBUJAMOS LA FIGURA GEOMÉTRICA QUE REPRESENTA AL “TODO”.

¿CUÁL ES EL DE DENOMINADOR? EL DENOMINADOR ES 4. ASÍ QUE DIVIDIMOS LA FIGURA EN 4 PARTES IGUALES.

¿CUÁL ES EL NUMERADOR? EL NUMERADOR ES 3. ENTONCES, COLOREAMOS 3 PARTES DE LA FIGURA.

¡ES TU TURNO!

REALIZA EL GRÁFICO DE ESTAS FRACCIONES:

$\boldsymbol{\frac{2}{5}}$

SOLUCIÓN

$\boldsymbol{\frac{2}{3}}$

SOLUCIÓN

LAS FRACCIONES SON UN TIPO ESPECIAL DE NÚMEROS Y SE LEEN DE UNA MANERA DIFERENTE A LOS DEMÁS. PRIMERO LEEMOS EL NUMERADOR COMO CUALQUIER NÚMERO NATURAL. EL DENOMINADOR CAMBIA SEGÚN EL NÚMERO, SI ES 2 SE LEE “MEDIOS”, SI ES 3 SE LEE “TERCIOS” Y SI ES 4 SE LEE “CUARTOS”. ASÍ, LA FRACCIÓN 1/2 SE LEE “UN MEDIO” Y LA FRACCIÓN 1/3 SE LEE “UN TERCIO”.

FRACCIONES EN LA VIDA COTIDIANA

LAS FRACCIONES FORMAN PARTE DE NUESTRO DÍA A DÍA. USAMOS FRACCIONES CADA VEZ QUE COMPRAMOS PAN, FRUTAS O VEGETALES, PUES PODEMOS PEDIR MEDIO KILOGRAMO DE ALGO. TAMBIÉN USAMOS FRACCIONES CUANDO DAMOS LA HORA Y DECIMOS, POR EJEMPLO, “SON LAS DOS Y CUARTO” LO QUE SIGNIFICA QUE HA PASADO 1/4 DE HORA DESPUÉS DE LAS 2.

– OTRAS SITUACIONES:

AL CORTAR UNA FRUTA EN DOS PARTES Y COMER UNA: $\frac{1}{2}$
AL CORTAR UNA PIZZA EN 4 PARTES Y COMER 2: $\frac{2}{4}$
AL COMPRAR PRODUCTOS: $\frac{1}{2}$ KILO DE HARINA.
AL REALIZAR UNA PARTE DE UN RECORRIDO. LAURA RECORRIÓ $\frac{3}{4}$ DE UNA CARRERA.

EN VARIAS SITUACIONES DE NUESTRA VIDA ENCONTRAMOS FRACCIONES DE FORMA GRÁFICA. UN EJEMPLO COMÚN DE FRACCIONES ES CUANDO REPARTIMOS UN PASTEL. EN LA IMAGEN VEMOS UNO CORTADO EN 8 PARTES IGUALES, ES DECIR, EL DENOMINADOR ES 8. TAMBIÉN VEMOS QUE SE TOMA 1 PARTE, ASÍ QUE EL NUMERADOR ES 1 Y LA FRACCIÓN DE ESE PEDAZO ES 1/8. LA TORTA TIENE FORMA DE CÍRCULO Y ES SIMILAR AL GRÁFICO DE LA FRACCIÓN.

¡A PRACTICAR!

ESCRIBE LA FRACCIÓN PARA CADA GRÁFICO:

SOLUCIÓN

PARTES EN LAS QUE SE DIVIDE AL ENTERO: 2

PARTES COLOREADAS: 1

FRACCIÓN: $\boldsymbol{\frac{1}{2}}$

SOLUCIÓN

PARTES EN LAS QUE SE DIVIDE AL ENTERO: 5

PARTES COLOREADAS: 1

FRACCIÓN: $\boldsymbol{\frac{1}{5}}$

SOLUCIÓN

PARTES EN LAS QUE SE DIVIDE AL ENTERO: 3

PARTES COLOREADAS: 2

FRACCIÓN: $\boldsymbol{\frac{2}{3}}$

SOLUCIÓN

PARTES EN LAS QUE SE DIVIDE AL ENTERO: 4

PARTES COLOREADAS: 3

FRACCIÓN: $\boldsymbol{\frac{3}{4}}$

SOLUCIÓN

PARTES EN LAS QUE SE DIVIDE AL ENTERO: 4

PARTES COLOREADAS: 2

FRACCIÓN: $\boldsymbol{\frac{2}{4}}$

RECURSOS PARA DOCENTES

Artículo “Fracciones”

Este recurso cuenta con ejemplos didáctico sobre los tipos de fracciones y cómo graficarlos.

VER

CAPÍTULO 5 / TEMA 2

REPRESENTACIÓN DE FRACCIONES

Todas las fracciones representan una división o las partes de un entero. Las usamos día a día cuando queremos repartir chocolates con amigos, una pizza con familiares y hasta picar una torta de cumpleaños para los invitados. Cada vez que organizamos una reunión y pensamos cuántos invitados vendrán, hacemos uso de las fracciones.

lectura de fracciones

Toda fracción tiene un numerador y un denominador. Podemos representarlos en esta caja de rosquillas. ¡Observa! La caja es el entero y lo dividimos en 12 partes iguales porque hay 12 rosquillas. Ese es el denominador. El numerador será igual a las rosquillas repartidas. Si solo repartirmos 4, podemos decir que comimos 4/12 de la caja.

Las fracciones reciben diferentes nombres de acuerdo a los números que aparecen en el numerador y el denominador. El numerador lo leemos como cualquier número natural y el denominador de la siguiente manera:

Denominador	Lectura
2	Medios
3	Tercios
4	Cuartos
5	Quintos
6	Sextos
7	Séptimos
8	Octavos
9	Novenos
10	Décimos

A partir del 11 el número se lee terminado en -avos. Por ejemplo, onceavos, doceavos, treceavos y así sucesivamente.

– Veamos algunos ejemplos:

$\boldsymbol{\frac{3}{7}}$ se lee “tres séptimos”.

$\boldsymbol{\frac{5}{3}}$ se lee “cinco tercios”.

$\boldsymbol{\frac{7}{12}}$ se lee “siete doceavos”.

$\boldsymbol{\frac{2}{10}}$ se lee “dos décimos”.

$\boldsymbol{\frac{8}{2}}$ se lee “ocho medios”.

¡Es tu turno!

Observa las siguientes fracciones, ¿cómo se leen?

$\boldsymbol{\frac{9}{4}}$

Solución

Nueve cuartos.

$\boldsymbol{\frac{25}{13}}$

Solución

Veinticinco treceavos.

$\boldsymbol{\frac{5}{8}}$

Solución

Cinco octavos.

representación gráfica

En una fracción, el denominador indica las partes en las que se divide al entero y el numerador las partes que se toman.

Estas definiciones son importantes para realizar los gráficos de fracciones.

¿Cómo graficar una fracción propia?

Realicemos el gráfico de la fracción $\boldsymbol{\frac{3}{5}}$

Lo primero que hacemos es dibujar una figura. En este caso dibujaremos un rectángulo. Este será el entero.

Luego dividimos el entero en la cantidad de partes que nos indique el denominador. En este caso, como el denominador es 5, dividimos el rectángulo en 5 partes iguales.

Después pintamos la cantidad de partes que señale el numerador. Como en esta fracción el numerador es 3, pintamos 3 partes. El resultado será el gráfico de la fracción.

¿Cómo graficar una fracción impropia?

La fracciones impropias tienen el numerador mayor al denominador y por lo tanto son mayores que 1.

Realicemos el gráfico de la fracción $\boldsymbol{\frac{6}{4}}$

Primero dibujamos un figura que represente al entero. En este caso es un cuadrado.

Ahora dividimos el entero en tantas partes como nos señale el denominador. El denominador de esta fracción es 4, así que dividimos al cuadrado en 4 partes iguales.

Luego pintamos las partes que nos indique el numerador. Como el numerador es 6, no es suficiente con una sola figura, así que dibujamos de nuevo otro cuadrado con 4 partes y pintamos las partes necesarias para llegar a 6. Ese será el gráfico de la fracción.

¿Sabías qué?

Siempre que el numerador sea mayor que el denominador será necesario que dibujemos más de un entero para representar la fracción.

¡A practicar!

Representa gráficamente las siguientes fracciones:

$\boldsymbol{\frac{4}{6}}$

Solución

$\boldsymbol{\frac{1}{4}}$

Solución

$\boldsymbol{\frac{7}{5}}$

Solución

representación en la recta numérica

La recta numérica es una línea recta sin principio ni final que contiene a todos los números. Ubicamos los números a partir del cero en segmentos iguales.

Entre el 0 y el 1, el 1 y el 2, o entre cualquier entero podemos encontrar fracciones. Todas estas también se pueden ubicar en la recta numérica.

Para ubicar las fracciones en la recta numérica solo tenemos que dividir la unidad en segmentos iguales según lo que indica el denominador y a partir del cero contamos tantos lugares como indique el numerador. Luego marcamos la fracción.

– Ejemplo:

Para representar en la recta numérica la fracción $\boldsymbol{\frac{2}{5}}$ sigue estos pasos:

Divide el espacio entre 0 y 1 en 5 partes iguales.
Cuenta desde el cero dos lugares porque el numerador es 2.
Ubica la fracción.

¿Sabías qué?

Para representar en la recta numérica fracciones impropias se usan fracciones mixtas. Estas fracciones están formadas por una parte entera y una fraccionaria.

Ubica las fracciones

¿Qué fracción se representa en esta recta numérica?

Solución

La fracción $\boldsymbol{\frac{7}{8}}$ .

Ubica en una recta numérica la fracción $\boldsymbol{\frac{2}{3}}$ .

Solución

VER INFOGRAFÍA

¿cómo se relacionan las fracciones y las divisiones?

Las fracciones son partes de un todo, es decir, son divisiones de ese todo. Por esta razón están directamente relacionadas una con la otra.

Toda fracción es una división sin resolver entre dos números: el numerador y el denominador.

Entonces, $\boldsymbol{\frac{1}{4}}$ es igual a $\boldsymbol{1\div 4}$ . Las dos son formas correctas de escribir una división.

¿Sabías qué?

Podemos expresar las fracciones con la raya horizontal o con una diagonal, por ejemplo, $\boldsymbol{\frac{3}{4}}$ es igual a $\boldsymbol{3/4}$ .

La representación de las horas

Un reloj analógico marca diferentes fracciones con el paso de las horas. En una hora hay cuatro cuartos de hora, así que, cuando decimos que pasaron 15 minutos después de las 12, realmente decimos que pasó 1/4 de hora. Cuando la aguja de los minutos (aguja larga) llega al 6 significa que pasó media (1/2) hora y a los 45 minutos pasaron 3/4 de una hora.

Actividades

1. ¿Cómo se lee la fracción 3/10? Realiza su gráfico.

Solución

3/10 se lee “tres décimos”.

Su gráfico es igual a este:

2. ¿Cómo se lee la fracción 5/12? Representa la fracción en la recta numérica.

Solución

5/12 se lee “cinco doceavos”.

En la recta se representa así:

3. Une cada fracción con su gráfico:

Solución

4. ¿Qué fracción está representada en la siguiente recta numérica?

Solución

La fracción 3/6.

5. ¿Qué fracción está representada en la siguiente recta numérica?

Solución

La fracción 1/5.

RECURSOS PARA DOCENTES

Artículo “Partes y porciones”

Este recurso permitirá profundizar la representación en la recta numérica.

VER

Video “Cómo se lee una fracción”

Este recurso audiovisual explica, de manera clara, los pasos a seguir para nombrar fracciones al tiempo que las compara con la unidad.

VER

CAPÍTULO 5 / TEMA 1

LOS PICTOGRAMAS

DESDE LA ANTIGÜEDAD, EL SER HUMANO HA INTENTADO COMUNICARSE A TRAVÉS DE PINTURAS EN CAVERNAS O CON TALLADOS EN METALES. LA NECESIDAD DE COMUNICARSE Y FALTA DE SÍMBOLO PARA ESCRIBIR LLEVARON AL HOMBRE A GRAFICAR LO QUE QUERÍA EXPRESAR A TRAVÉS DE DIBUJOS. A ESTAS REPRESENTACIONES HOY SE LAS LLAMAN PICTOGRAMAS.

¿QUÉ SON LOS PICTOGRAMAS?

UN PICTOGRAMA ES UN TIPO DE GRÁFICO QUE SE REPRESENTA A TRAVÉS DE DIBUJOS. EN LA ACTUALIDAD ES ENTENDIDO COMO UN AVISO CLARO DE UNA CIERTA INFORMACIÓN QUE SE NECESITA EXPRESAR.

LA SEÑALES DE TRÁNSITO

LAS SEÑALES DE TRÁNSITO RESULTAN DE LA COMBINACIÓN DE FORMAS GEOMÉTRICAS Y COLORES A LAS QUE SE LES AÑADE UN SÍMBOLO O PICTOGRAMA QUE TIENE UN SIGNIFICADO RELACIONADO A LA SEGURIDAD EN EL TRÁFICO. ESTOS PICTOGRAMAS SIRVEN PARA COMUNICAR DE FORMA SIMPLE Y RÁPIDA UNA INFORMACIÓN A CUALQUIER PERSONA DEL MUNDO.

¿SABÍAS QUÉ?

LAS HISTORIETAS, CÓMICS Y LOS CHISTES GRÁFICOS QUE NO TIENEN TEXTO TAMBIÉN SON PICTOGRAMAS.

INFORMACIÓN A TRAVÉS DE PICTOGRAMAS

LOS PICTOGRAMAS SON ÚTILES PARA REPRESENTAR DATOS. SI TENEMOS UNA TABLA CON PICTOGRAMAS LO PRIMERO QUE TENEMOS QUE VER ES LA CLAVE O LEYENDA.

– EJEMPLO:

MARÍA VENDIÓ HELADOS DE CHOCOLATE DURANTE 4 SEMANAS. DESPUÉS DE CONTAR SUS VENTAS SE OBTUVO LA SIGUIENTE TABLA:

COMO CADA DIBUJO REPRESENTA 5 UNIDADES, TENEMOS QUE MULTIPLICAR LA CANTIDAD DE DIBUJOS POR 5, DE ESTA MANERA SABREMOS LA CANTIDAD TOTAL DE HELADOS EN CADA SEMANA.

¡ES TU TURNO!

OBSERVA EL PICTOGRAMA ANTERIOR Y RESPONDE:

¿EN CUÁL SEMANA MARÍA VENDIÓ MÁS HELADOS DE CHOCOLATE?
SOLUCIÓN
EN LA SEGUNDA SEMANA.

¿EN CUÁL SEMANA VENDIÓ MENOS HELADOS DE CHOCOLATE?
SOLUCIÓN
EN LA CUARTA SEMANA.

¿CUÁNTOS HELADOS DE CHOCOLATE VENDIÓ LA PRIMERA SEMANA?
SOLUCIÓN
15 HELADOS.

– EJEMPLO 2:

EN UNA ESCUELA SE CONTARON LOS ESTUDIANTES QUE PRACTICAN ALGÚN DEPORTE Y SE OBTUVO ESTA TABLA:

¡ES TU TURNO!

OBSERVA EL PICTOGRAMA ANTERIOR Y RESPONDE:

¿EN CUÁL GRADO HAY MÁS ESTUDIANTES QUE PRACTICAN ALGÚN DEPORTE?
SOLUCIÓN
EN 5º.

¿EN CUÁL GRADO HAY MENOS ESTUDIANTES QUE PRACTICAN ALGÚN DEPORTE?
SOLUCIÓN
EN 1º.

¿CUÁNTOS ESTUDIANTES PRACTICAN ALGÚN DEPORTE EN TOTAL?
SOLUCIÓN
4 + 8 + 16 + 12 + 20 + 12 = 72
72 ESTUDIANTES PRACTICAN ALGÚN DEPORTE.

GRAFICAR INFORMACIÓN EN PICTOGRAMAS

PARA GRAFICAR INFORMACIÓN EN UN PICTOGRAMA ES NECESARIO QUE:

SEPAMOS LOS DATOS.
ESCOJAMOS UN DIBUJO.
DEMOS UN VALOR A CADA DIBUJO.
DIBUJEMOS UNA TABLA.
COLOQUEMOS LOS DIBUJOS Y LAS CUENTAS DENTRO DE LA TABLA.

– EJEMPLO:

MARCOS VENDIÓ 12 PANES EL LUNES, 9 PANES EL MARTES Y 6 PANES EL MIÉRCOLES. GRAFIQUEMOS CON PICTOGRAMAS ESTOS DATOS.

SI NOS UBICAMOS EN LA TABLA DEL 3, VEMOS QUE PODEMOS OBTENER TODOS LOS RESULTADOS POR MEDIO DE MULTIPLICACIONES CON ESTE NÚMERO. ASÍ QUE LA CLAVE ES ASÍ:

AHORA SOLO TENEMOS QUE REALIZAR UNA TABLA EN LA QUE SE OBSERVEN LOS DÍAS Y LA CANTIDAD DE PANES EQUIVALENTES A LAS VENTAS.

¡A PRACTICAR!

1. COMPLETA ESTE PICTOGRAMA. LUEGO RESPONDE:

SOLUCIÓN

¿EN QUÉ MES SE VENDIERON MÁS TORTAS?
SOLUCIÓN
EN ENERO.

¿EN QUÉ MES SE VENDIERON MENOS TORTAS?
SOLUCIÓN
EN FEBRERO.

¿CUÁNTAS TORTAS SE VENDIERON EN LOS TRES MESES?
SOLUCIÓN
30 + 10 + 20 = 60
SE VENDIERON 60 TORTAS.

¿EN QUÉ MES SE VENDIERON 20 TORTAS?
SOLUCIÓN
EN MARZO.

¿EN QUÉ MES SE VENDIERON MENOS DE 20 TORTAS?
SOLUCIÓN
EN FEBRERO.

RECURSOS PARA DOCENTES

Artículo “Gráficos estadisticos”

Este recurso brinda más información sobre los gráficos y sus tipos, incluidos los pictogramas.

VER

CAPÍTULO 5 / TEMA 8 (REVISIÓN)

Geometría y mediciones | ¿Qué aprendimos?

Perímetro

El perímetro es el contorno de una figura geométrica. En el caso de los polígonos regulares, el perímetro lo calculamos al multiplicar la cantidad de sus lados por la longitud de uno de estos. Otra forma de calcular el perímetro es a través de la suma de cada uno de los lados de una figura. En cambio, el perímetro del círculo es igual a la multiplicación del número pi por el diámetro de la circunferencia. Existen también figuras compuestas que están formadas por dos o más figuras geométricas, para calcular su perímetro basta con sumar cada uno de los lados.

Ángulos

Uno de los elementos fundamentales para la geometría es el ángulo, el cual está formado por un par de semirrectas denominadas lados que tienen un origen común o vértice. Uno de los sistemas más usados para medir ángulos es el sistema sexagesimal, en el que medimos los ángulos en grados, minutos y segundos. De acuerdo a su tamaño, los ángulos pueden clasificarse en agudos, rectos, obtusos y llanos. Los agudos son mayores a 0° pero menores a 90°, los rectos miden 90°, los obtusos son mayores a 90° pero menores de 180° y los llanos miden siempre 180°.

Área

Para calcular superficies usamos el área, que es la extensión comprendida por una figura. Para cada figura plana existe una fórmula que permite determinar su área. En el Sistema Internacional de Unidades se emplea el metro cuadrado (m²) como unidad de medida de área, pero también podemos usar otras unidades derivadas, como el centímetro cuadrado (cm²) o el milímetro cuadrado (mm²). Podemos obtener el área de las figuras compuestas al descomponerlas en figuras geométricas más simples, para luego sumar las áreas de cada una.

Sistemas de referencia

Uno de los sistemas de referencias más usados es el sistema cartesiano, el cual está formado por dos ejes en el plano: uno horizontal denominado eje X o de las abscisas y otro vertical denominado eje Y o de las ordenadas. Para representar un punto en el plano cartesiano necesitamos sus coordenadas en el eje X y en el eje Y: la intersección de ambas coordenadas constituye su ubicación. Por otro lado, las figuras pueden experimentar transformaciones isométricas, es decir, cambios de posición y orientación que no afectan su forma. Estas transformaciones son: traslación, rotación y simetría.

Cuadriláteros

Un cuadrilátero es un polígono de cuatro lados, y aunque se pueden clasificar en varios grupos, comparten elementos en común: tienen cuatro ángulos, la suma de estos es siempre igual 360° y tienen dos diagonales que dividen al cuadrado en triángulos. De manera general, los cuadriláteros son clasificados como paralelogramos, trapecios y trapezoides. Los paralelogramos tienen sus lados opuestos paralelos y pueden ser cuadrados, rombos y rectángulos. Los trapecios tienen dos de sus lados paralelos y los trapezoides no tienen ningún lado paralelo.

El campo de fútbol tiene forma de rectángulo que es un tipo de cuadrilátero.

Capacidad y volumen

El volumen es el espacio que ocupa un objeto mientras que la capacidad indica la cantidad que un objeto puede contener dentro de él. Todos los objetos tienen volumen pero no todos tienen capacidad. En el caso de los sólidos y los líquidos mientras mayor sea su volumen, mayor espacio van a ocupar. No es lo mismo el volumen de un grano de arroz que el de un edificio. Algunas unidades de volumen son el metro cúbico (m³), el centímetro cúbico (cm³) y milímetro cúbico (mm³), entre otras. El litro es una medida de capacidad que equivale a 1.000 cm³.

A pesar de estar muy relacionadas, no se deben confundir las medidas de volumen con las de capacidad.

La circunferencia

La circunferencia es una curva plana con todos sus puntos ubicados a la misma distancia del origen o centro. No debe ser confundida con el círculo que corresponde al área contenida dentro de ella, es decir, la circunferencia es el perímetro del círculo. Presenta ciertos elementos como el radio, el diámetro, la tangente, la cuerda, el arco y la semicircunferencia. Uno de los instrumentos usados para su trazado es el compás.

CAPÍTULO 5 / TEMA 7

La circunferencia

Una de las curvas más estudiadas en la geometría es, sin duda, la circunferencia. Tiene características únicas y ha sido pieza fundamental en invenciones humanas como la rueda. Para trazar esta figura usamos el compás, y su longitud está determinada por un número muy particular: el número pi.

¿Qué es una circunferencia?

Es la curva plana y cerrada cuyos puntos equidistan del centro; es decir, están a la misma distancia del centro de la circunferencia.

Los griegos y la circunferencia

Sin lugar a duda, los antiguos griegos tuvieron una gran influencia en el perfeccionamiento de la geometría. Para ellos, la línea recta y la circunferencia eran muy importantes en sus construcciones matemáticas, lo que permitió que realizaran increíbles descubrimientos para su época. Por ejemplo, Eratóstene de Cirene, que vivió entre 276 y 194 a. C., fue la primera persona en calcular la circunferencia de la Tierra.

Elementos de la circunferencia

En la circunferencia se pueden observar los siguientes elementos:

Centro: es el punto en torno al cual equidistan todos los puntos de la curva.

Radio: es un segmento de recta que une el centro de la circunferencia con cualquiera de sus puntos.

Diámetro: es un segmento de recta que une a dos puntos de la circunferencia y pasa por el centro de la misma. Su longitud es igual al doble del radio.

Cuerda: es un segmento de recta que une a dos puntos de la circunferencia sin pasar por el centro.

Arco: es una porción de la circunferencia que se encuentra limitada por una cuerda.

Semicircunferencia: es la porción de circunferencia limitada por el diámetro. Equivale a la mitad de la circunferencia.

Posiciones de una recta en relación a la circunferencia

Recta tangente: es la recta que comparte un mismo y único punto con la circunferencia.

Recta secante: es la recta que comparte dos puntos con la circunferencia.

Recta exterior: es la recta que no comparte ningún punto con la circunferencia.

¿Sabías qué?

La circunferencia de la tierra mide cerca de 40.000 km de longitud.

Diferencia entre círculo y circunferencia

Es posible que confundamos los conceptos de círculo y circunferencia porque están muy relacionados entre sí, pero se trata de dos términos diferentes. El círculo es una figura plana que corresponde al área contenida dentro de una circunferencia. La circunferencia, por su parte, representa el perímetro del círculo, es decir, es la línea que forma el contorno de la figura.

VER INFOGRAFÍA

El círculo es una figura que presenta diferentes elementos, como el semicírculo, los sectores circulares y los segmentos circulares. El primero es el área comprendida entre el diámetro y una semicircunferencia; el segundo consiste en las regiones comprendidas entre dos radios y el arco que estos forman; y el tercero se trata de los segmentos que se forman entre una cuerda y su arco.

Trazado de circunferencias

El compás es el instrumento por excelencia para trazar circunferencias y su origen es muy antiguo. Un compás consta de los siguientes elementos principales:

Un mango.
Una punta metálica.
Una punta trazadora.
Dos brazos regulables.

El uso de esta herramienta es relativamente sencillo. Para trazar una circunferencia con un compás lo primero que debemos hacer es conocer el radio de la circunferencia y trazarlo con la ayuda de una regla. Luego posicionamos la punta metálica en uno de los extremos del segmento y luego abrimos los brazos hasta que la punta trazadora esté ubicada en el otro extremo del segmento. Finalmente, con ayuda del mango, trazamos la circunferencia.

Circunferencias a nuestro alrededor

Un anillo o un aro son ejemplos de circunferencias, pero hay muchos más. Al ser una circunferencia el contorno de un círculo, la observamos en los bordes de las ruedas de los autos, en un molde para hacer una torta o un pastel y hasta incluso en juguetes como los platos voladores.

Las circunferencias han sido elementos fundamentales en el desarrollo de la geometría y con ello también han permitido a los seres humanos realizar grandes invenciones como la rueda.

La circunferencia es el contorno de una de las figuras más comunes: el círculo. Es frecuente observarlas en platos, ruedas, pasteles, diseños y pinturas. Han permitido realizar cálculos y aproximaciones, como el descubrimiento del número pi que relaciona la longitud de la circunferencia con su radio y que ha tenido numerosas aplicaciones prácticas.

¡A practicar!

Además del centro, ¿qué elementos de la circunferencia observas?

Solución

Diámetro.

Solución

Arco.

Solución

Cuerda.

Solución

Radio.

2. ¿Cuál de las siguientes rectas es una tangente?

Solución

Es tangente porque solo comparte un punto en común con la circunferencia.

RECURSOS PARA DOCENTES

Artículo “Circunferencia”

El siguiente artículo explica de forma resumida qué es una circunferencia y los diferentes elementos que la integran como el radio, la cuerda, el diámetro, etc.

VER

Artículo “Ángulos en la circunferencia”

Este artículo relaciona los conceptos de ángulo y circunferencia, así como también explica sus características.

VER

CAPÍTULO 5 / TEMA 4

Sistemas de referencia

Son convencionalismos adoptados por el ser humano para medir la posición y otras magnitudes físicas. Se usan para hallar cuerpos celestes en el espacio y son la base para determinar nuestra ubicación en el planeta. También permiten establecer comparaciones y transformaciones entre las figuras representadas.

Ejes de coordenadas

El sistema de coordenadas cartesianas es uno de los sistemas de referencias usados para ubicar puntos en el espacio. En este caso específicamente se explicarán estas coordenadas orientadas al plano, es decir, en dos dimensiones.

El plano donde ubicamos los puntos se denomina plano cartesiano y está formado por los siguientes elementos:

Eje X: es también denominado eje de las abscisas, y se encuentra ubicado dentro del plano en forma horizontal.
Eje Y: es conocido también como eje de las ordenadas y está ubicado en sentido vertical dentro del plano.
Origen: es el punto de intersección entre los ejes de coordenadas X e Y.

Los ejes de coordenadas permiten ubicar puntos, gráficos o figuras dentro del plano cartesiano. Al tratarse de dos ejes: el de las abscisas o eje X y el de las ordenadas o eje Y, se requieren de dos coordenadas para ubicar un punto, es decir, un punto está definido dentro del plano si, y solo si, se conocen sus coordenadas en el eje X y en el eje Y.

¿Sabías qué?

El nombre de las coordenadas cartesianas proviene de la persona que las empleó por primera vez: René Descartes.

VER INFOGRAFÍA

¿Cómo graficar un punto en el plano cartesiano?

Un punto está definido por un par de números que hacen referencia a su posición respecto al eje X y al eje Y. Estos puntos son denominados coordenadas cartesianas y permiten graficarlo.

Para hacerlo, dividimos los ejes en segmentos con la misma longitud y a cada uno le asignamos el valor de un número entero. A la derecha del origen, escribimos los números de menor a mayor, esos serán los valores del eje X. Arriba del origen escribimos los números que le siguen al cero de menor a mayor, esos serán los valores del eje Y:

¿Sabías qué?

Los números negativos se representan a la izquierda del origen (eje X) y debajo del origen (eje Y).

Para ubicar un punto en el plano necesitamos las coordenadas de cada eje, que de ahora en adelante llamaremos coordenada en X y coordenada en Y para hacer mención a cuál eje se refieren. La coordenada X determina cuán a la derecha del origen está ubicado el punto; mientras que la coordenada Y, cuán arriba del origen está el punto.

La manera más frecuente de representar un punto es a través de paréntesis, y dentro indicamos la coordenada X y la coordenada Y, separadas por una coma:

$\left ( Coordenada \, X,\, Coordenada\, Y \right )$

El punto desde dónde se empieza a contar es en el origen porque se encuentra en la coordenada (0,0) lo que quiere decir que está a 0 posiciones de la derecha y a 0 posiciones hacia arriba.

Por ejemplo:

El punto A (3,2) se encuentra a tres posiciones a la derecha y a dos posiciones hacia arriba. Si lo queremos graficar, cada coordenada debe estar representada en el respectivo eje y el punto de intersección de ambas sería el punto A:

Cuando algunas de las coordenadas del punto sea igual a cero, significa que el punto se encuentra sobre el eje al cual corresponde la coordenada diferente de cero. Por ejemplo, el punto B (0,3) indica que se movió cero posiciones a la derecha y tres posiciones hacia arriba, por lo tanto se ubica sobre el eje Y que es el que tiene la coordenada diferente de cero:

Ejes de simetrías

La simetría es una relación proporcionada entre las partes que componen un todo. Así, por ejemplo, decimos que una imagen es simétrica cuando su forma no cambia si es girada o volteada. Para que exista simetría entre dos objetos, ambos deben ser del mismo tamaño y de la misma forma y uno debe estar en una orientación diferente a la del primero.

La forma de una mariposa es un ejemplo de simetría: si trazamos una línea imaginaria de forma vertical en el centro de la mariposa (eje de simetría), obtendríamos dos imágenes iguales pero con diferente orientación. Nuestros cuerpos también son simétricos: esto se debe a que contamos con la misma cantidad de miembros a cada lado.

El eje de simetría es una línea imaginaria que divide al dibujo en dos partes idénticas pero con diferente orientación. Los ejes de simetría pueden ser horizontales, verticales o inclinados.

De acuerdo a la figura geométrica, algunas pueden presentar uno o más ejes de simetría. Otras, en cambio, no presentan ninguno. Cuando una figura no es simétrica se denomina asimétrica.

Por ejemplo, no todos los triángulos tienen ejes de simetría, todo depende de su tipo. Si son equiláteros tienen tres ejes de simetría; si son isósceles tienen dos ejes de simetría, y si son escalenos no tienen ningún eje de simetría.

Transformaciones isométricas

Las transformaciones isométricas son los cambios de posición u orientación que experimenta una figura sin alterar su forma.

Traslación

Es un tipo de transformación isométrica donde se mueven todos los puntos de una figura en una misma dirección, sentido y longitud.

Rotación

También es conocida como giro. Es una transformación isométrica en la que la figura se mueve alrededor de un punto sin alterar su forma. El movimiento es determinado por un ángulo de rotación y puede ser en sentido de las agujas del reloj o en sentido contrario.

La simetría como transformación isométrica

La simetría entre dos objetos es un tipo de transformación isométrica porque a cada punto del objeto o figura se lo asocia a otro conocido como imagen. Cada punto está a una misma distancia del otro respecto al eje de simetría. Este tipo de transformación también se conoce como reflexión.

¡A practicar!

1. ¿Cuál es la posición de estos números?

Solución

C (4,3)

Solución

D (1,2)

Solución

E (5,0)

Solución

F (4,5)

Solución

G (3,3)

2. ¿A cuál de los siguientes puntos corresponde la coordenada (6,3)?

Solución

Corresponde al punto K (6,3).

3. ¿Cuál de estas figuras no es simétrica?

Solución

No es simétrica porque no tiene ningún eje de simetría.

4. ¿A qué tipo de transformación isométrica corresponde la gráfica?

Solución

Traslación.

RECURSOS PARA DOCENTES

Artículo “Simetrías”

Este artículo explica qué es una simetría, sus tipos y su relación con los ejes. También incluye algunos ejemplos de simetría.

VER

Artículo “Plano cartesiano”

Este artículo explica qué es el plano cartesiano, sus características y divisiones por cuadrante. También incluye ejemplos sobre como ubicar puntos en este sistema.

VER

CAPÍTULO 3 / TEMA 6 (REVISIÓN)

Fracciones | ¿Qué aprendimos?

¿Qué son las fracciones?

Una fracción está formada por dos términos principales: el numerador y el denominador. Estos son números enteros que están separados por una línea horizontal denominada raya divisoria o raya fraccionaria. Una fracción es la división de un entero o una unidad en partes iguales. El numerador indica las partes a considerar de esa división y el denominador indica las partes en las que se dividió el entero o unidad. Estos números son más antiguos que lo que se piensa y están relacionados con la división.

Fracciones diversas

De acuerdo a la relación que exista entre el numerador y el denominador, las fracciones pueden ser propias o impropias. Las fracciones propias son aquellas en las que el numerador es menor que el denominador, contrario a las fracciones impropias, en las que el numerador es mayor que el denominador. Por otro lado, si comparamos dos o más fracciones, estas pueden ser homogéneas o heterogéneas. Las fracciones homogéneas son las que poseen el mismo denominador, las heterogéneas, en cambio, presentan diferentes denominadores.

Las fracciones pueden expresarse en forma de gráfica o viceversa. Lo emocionante de ellas es que las usamos a diario para dividir cosas o cantidades.

Gráficas de fracciones

Las fracciones suelen expresarse en gráficos para interpretar de manera más sencilla los datos. La forma para representar estos gráficos dependen del tipo de fracción. Si la fracción es propia elegimos cualquier figura, la dividimos en partes iguales según el denominador y señalamos las partes que indique el numerador. Cuando se trata de una fracción impropia dividimos una figura geométrica en las partes que señale el denominador, pero debido a que en este tipo de fracción el numerador es mayor que el denominador, serán necesarias más de una figuras.

Los números mixtos son un tipo de número fraccionario que posee una parte entera y otra fraccionaria.

Orden de fracción

Las fracciones presentan un sentido de orden, es decir, hay fracciones que son mayores o menores que otras. Una herramienta muy útil para reconocer este orden es la recta numérica. Se trata de un gráfico en forma de línea horizontal en el que los números están ordenados de menor a mayor. Para ubicar fracciones propias en la recta numérica dividimos la unidad en segmentos iguales según indique el denominador y la fracción se ubicaría en el número de segmento indicado por el numerador. Las fracciones impropias, por su parte, deben ser transformadas en números mixtos.

En la recta numérica, si se toma un número como referencia, los números de su izquierda son menores a él y los de la derecha mayores.

Problemas con fracciones

Las fracciones, además de ayudarnos a resolver problemas que impliquen proporciones, nos permiten resolver las operaciones básicas matemáticas como la adición, la sustracción, la multiplicación y al división. En el caso de la adición y la sustracción de fracciones debemos tener en cuenta su tipo: si las fracciones son homogéneas sumamos o restamos los numeradores y colocamos el denominador, si son heterogéneas usamos el método de cruz para resolverlas. Las multiplicaciones se resuelven de forma lineal, al multiplicar los numeradores y los denominadores.

La adición y sustracción de fracciones heterogéneas suele realizarse por el método en cruz que permite calcular de manera directa fracciones equivalentes.

CAPÍTULO 3 / TEMA 4

Orden de Fracción

Las fracciones forman parte del conjunto de números racionales. Estos números pueden ser expresados como cociente de un número entero y un número natural. Todos los números siguen una secuencia, por lo tanto, es posible ordenarlos en la recta numérica y determinar cuál número es mayor, menor o igual a otro.

Ordenar fracciones en la recta numérica

La recta numérica es un recurso muy útil para comparar números. Consiste en un gráfico en forma de línea en el que se ordenan los números de menor a mayor en sentido de izquierda a derecha.

Las fracciones propias (las que tienen el numerador menor que el denominador) son las más fáciles de graficar porque solo tienes que dividir la unidad en tantos segmentos iguales como indique el denominador y luego, según el numerador, contar los segmentos y ubicar la fracción en la recta.

Por ejemplo, si queremos graficar la fracción $\frac{5}{6}$ , tenemos que dividir la unidad en seis segmentos iguales:

Para ubicar la fracción contamos los segmentos que nos indique el numerador, como en este caso el numerador es cinco (5), se cuentan cinco segmentos a partir del cero:

Por medio del diagrama anterior también podemos graficar la fracción $\frac{1}{6}$ , que es una fracción que comparte el mismo denominador con la fracción $\frac{5}{6}$ ya ubicada en la gráfica. Al seguir los mismos pasos anteriores se obtiene:

Las fracciones con el mismo denominador se pueden comparar fácilmente, la que tenga el numerador mayor será también la mayor fracción. Es por eso que $\frac{5}{6}$ es mayor que $\frac{1}{6}$ .

¿Sabías qué?

En la recta numérica, un número es mayor a los números ubicados a su izquierda y menor a los ubicados a su derecha.

¿Qué hacer si tenemos dos fracciones con denominadores diferentes?

Cuando existan dos fracciones con denominadores diferentes multiplicamos el numerador y denominador de la primera fracción por el denominador de la segunda fracción, y así, tendremos una fracción equivalente. Luego se hace lo mismo con la segunda fracción pero se multiplica su numerador y denominador por el denominador de la primera fracción.

Las dos fracciones obtenidas tendrán el mismo denominador y de esta manera, solo queda ubicar la fracción en la recta tal como se explicó en el punto anterior.

Por ejemplo, si queremos ubicar las fracciones $\frac{1}{2}$ y $\frac{3}{4}$ en la recta numérica, no podemos dividir la recta en segmentos iguales porque no comparten el mismo denominador. Entonces determinamos fracciones equivalentes de cada una, es decir, calculamos fracciones que con diferente valor de numerador y denominador representan la misma cantidad.

Para calcular la fracción equivalente de $\frac{1}{2}$ multiplicamos su numerador y denominador por el denominador de la segunda fracción que es cuatro (4):

$\frac{1\times 4}{2\times 4}= \frac{4}{8}$

En este sentido, la fracción $\frac{4}{8}$ es equivalente a $\frac{1}{2}$ .

Calculamos ahora la fracción equivalente de $\frac{3}{4}$ que se obtiene al multiplicar su numerador y denominador por el denominador de la primera fracción que es dos (2).

$\frac{3\times 2}{4\times 2}= \frac{6}{8}$

De esta manera obtenemos la fracción $\frac{6}{8}$ que es equivalente con $\frac{3}{4}$ .

Las fracciones $\frac{4}{8}$ y $\frac{6}{8}$ son equivalentes con las fracciones anteriores. Observemos que tienen el mismo denominador y para poder ubicarlas en la recta numérica debemos dividir la unidad en 8 segmentos iguales, después escribimos cada fracción en el número de segmento que indique su respectivo numerador. El gráfico quedaría:

Como $\frac{4}{8}$ representa la misma cantidad que $\frac{1}{2}$ , y $\frac{6}{8}$ representa la misma cantidad que $\frac{3}{4}$ . Estas fracciones pueden ser sustituidas en la recta numérica anterior:

De la imagen anterior se puede que concluir que $\frac{3}{4}$ es mayor que $\frac{1}{2}$ por estar ubicado a su derecha.

La recta numérica es una herramienta muy usada para ordenar y observar de manera más sencilla los datos. Este simple gráfico, además de los números naturales, permite ubicar números negativos, números racionales y números irracionales. Hay disciplinas como la física que emplean este tipo de diagrama para resolver problemas de cuerpos en movimiento.

¿Qué hacer si la fracción es impropia?

Si la fracción es impropia (aquella que su numerador es mayor que el denominador) se debe transformar a un número mixto: un número formado por una parte entera y una fracción. En la gráfica, la fracción impropia estará ubicada entre el número entero del número mixto y el número siguiente de la recta. La ubicación exacta la proporciona la parte fraccionaria y la graficamos como se explicó en los casos anteriores.

Pasos para transformar una fracción impropia a un número mixto

1. Divide el numerador entre el denominador.

2. Escribe el cociente de la división anterior, el mismo será la parte entera del número mixto.

3. Escribe al lado de la parte entera la fracción del número mixto. En esta, el numerador será igual al resto de la división y el denominador será el mismo de la fracción original.

– Grafiquemos la fracción $\frac{5}{3}$

Lo primero es transformar la fracción a número mixto, para esto solo debes dividir el numerador entre el denominador:

El número mixto será $1\frac{2}{3}$ . Observa que:

La parte entera es el cociente de la división: 1.
El numerador de la parte fraccionaria es el resto: 2.
El denominador de la parte fraccionaria es el mismo de la fracción original: 3.

Ahora que tenemos nuestro número mixto sabemos que la fracción se encuentra ubicada entre el 1 y el 2 de la recta numérica, pero no sabemos en qué lugar. Para ello debemos hacer los mismos pasos que hicimos inicialmente para graficar fracciones, es decir, dividir el entero o unidad (que en este caso será el intervalo comprendido entre 1 y 2. Como el divisor es tres (3) entonces dividimos el intervalo en tres segmentos iguales:

Luego ubicamos la fracción de acuerdo a la cantidad de segmentos que indique el numerador. De esta manera, el número mixto que es igual a la fracción original se ubicaría así:

Relación de orden entre fracciones y naturales

Los números que se representan en la recta numérica cumplen el mismo criterio: los números de la izquierda de un número son menores a este y los de su derecha son mayores. Es por ello que representar las fracciones en la recta es de gran utilidad, pues permite relacionar los números de manera más fácil.
En el ejemplo anterior, la fracción $\frac{5}{3}$ se ubica en la gráfica entre el número 1 y el número 2. De esta manera, la fracción es mayor a 1 por estar a su derecha pero es menor que 2 por estar a su izquierda.

Uso de los símbolos “>” y “<“

Hay números naturales o fraccionarios que representan una mayor cantidad que otros. Por ejemplo, no es lo mismo decir 3 computadoras que decir 1.500 computadoras. Esta relación entre los números se denomina orden y nos permite diferenciar números mayores o menores.

En la práctica se emplean los símbolos “>” y “<” para denotar el orden de los números:

Símbolo	Significado
>	Mayor que
<	Menor que

Por ejemplo, el 5 es mayor que el 2, entonces, se puede expresar como $5> 2$ . Por otro lado, el número 3 es menor que el 9, en este caso se expresaría como $3<9$ .

La misma teoría es aplicada a las fracciones. De los ejemplos anteriores tenemos que:

a) $\frac{3}{4}> \frac{1}{2}$

b) $\frac{5}{3}<2$

¿Cómo reconocer cuando una fracción es menor o mayor que otra?

Si las fracciones tienen el mismo denominador, se comparan los numeradores, el numerador mayor corresponde a la fracción mayor. Por ejemplo:

a) $\frac{5}{2}> \frac{3}{2}$

b) $\frac{2}{7}< \frac{6}{7}$

Si las fracciones tienen denominadores diferentes, se convierten ambas en fracciones equivalentes con el mismo denominador. Por ejemplo, las fracciones $\frac{3}{5}$ y $\frac{5}{2}$

$\frac{3}{5}\rightarrow \frac{3\times 2}{5\times 2}= {\color{Red} \frac{6}{10}}$

$\frac{5}{2}\rightarrow \frac{5\times 5}{2\times 5}= {\color{Red} \frac{25}{10}}$

En este ejemplo, como $\frac{6}{10}< \frac{25}{10}$ , entonces $\frac{3}{5}< \frac{5}{2}$ .

Las fracciones equivalentes son aquellas que aunque tengan diferente numerador y denominador, representan la misma cantidad. Son útiles para comparar fracciones y también para simplificar operaciones, como la suma de fracciones con diferentes denominadores. Existen varias formas de calcularlas, como el método del mínimo común múltiplo.

¡A practicar!

1. ¿Qué fracción representa la siguiente gráfica?

a) $\frac{6}{2}$

b) $\frac{3}{1}$

c) $\frac{3}{6}$

d) $\frac{3}{2}$

Solución

c) $\frac{3}{6}$

2. ¿Cuál de las siguientes imágenes representa la gráfica de la fracción $\frac{5}{9}$ ?
a)

Solución

3. ¿Cuál de las siguientes fracciones es mayor?

a) $\frac{9}{10}$ y $\frac{7}{10}$

Solución

$\frac{9}{10}$

b) $\frac{3}{2}$ y $\frac{1}{4}$

Solución

$\frac{3}{2}$

4. ¿Cuál de las siguientes fracciones es menor?

a) $\frac{2}{5}$ y $\frac{1}{2}$

Solución

$\frac{2}{5}$

b) $\frac{7}{4}$ y $\frac{9}{6}$

Solución

$\frac{9}{6}$

5. Completa la expresión con los símbolos “>” y “<“.

a) $\frac{3}{2}\sqsubset \sqsupset \frac{1}{2}$

Solución

b) $\frac{5}{9}\sqsubset \sqsupset \frac{8}{9}$

Solución

c) $\frac{5}{2}\sqsubset \sqsupset \frac{7}{4}$

Solución

d) $\frac{1}{9}\sqsubset \sqsupset \frac{3}{8}$

Solución

RECURSOS PARA DOCENTES

Artículo “La recta numérica”

En este artículo destacado se explica con mayor detalle qué es la recta numérica y cómo representar en ella varios tipos de números como los fraccionarios.

VER

Artículo “Comparar y ordenar números”

El presente artículo permite conocer los símbolos usados en la comparación de números y muestra una serie de ejemplos de acuerdo a la cantidad de dígitos o cifras.

VER

CAPÍTULO 3 / TEMA 3

Gráficas de fracciones

Las gráficas son recursos visuales que permiten representar datos numéricos, como las fracciones. En este tipo de problemas podemos usar gran variedad de figuras para expresar una fracción de manera más sencilla, y así facilitar su interpretación. Los pasos para poder graficar una fracción dependen de su tipo.

Graficar una fracción propia

Podemos expresar fracciones a través de diagramas, pero para comprender cómo realizar un gráfico es importante recordar que una fracción es la representación de una o varias partes iguales de la unidad, donde:

El denominador representa el número de partes que se dividen de la unidad.

El numerador es el número de partes que se toman o se consideran de la unidad.

Toda fracción propia cumple una condición: el numerador siempre es menor que el denominador.

Pasos para graficar una fracción propia

Elige la figura en la que se va a representar la fracción. Puede ser un triángulo, círculo, cuadrado, rectángulo, etc.
Divide la figura elegida en tantas partes como indique el denominador de la fracción. Todas las partes deben ser iguales.
Señala el número de partes que indique el numerador de la fracción.

– Grafica la fracción $\frac{3}{4}$

La figura que seleccionaremos en este caso será un triángulo, pero recuerda que puede ser cualquier figura. Como el denominador de la fracción es cuatro (4), la figura debe estar dividida en cuatro partes iguales:

Luego señalamos el número de partes que indique el numerador, en este caso serían tres (3) partes:

De manera gráfica es más fácil entender la representación de la fracción “tres cuartos”.

Otros ejemplos:

¿Sabías qué?

Las fracciones no solo pueden representarse con figuras geométricas, también lo pueden hacer en la recta numérica.

¿Cómo graficar fracciones cuyo numerador es igual al denominador?

A este tipo de fracción se lo denomina fracción igual la unidad porque, al ser iguales el numerador y el denominador, el cociente de ambos siempre va a ser uno (1). Por esta razón la representamos como toda la figura geométrica:

VER INFOGRAFÍA

Graficar una fracción impropia

En las fracciones impropias el numerador siempre es mayor al denominador y, como su resultado es mayor a la unidad, se requiere más de una figura geométrica para representarlas.

Pasos para graficar una fracción impropia

Elige la figura en la que se va a representar la fracción.
Divide la figura elegida en tantas partes como indique el denominador de la fracción. Todas las partes deben ser iguales.
Señala el número de partes que indique el numerador de la fracción. Como es una fracción impropia van a faltar partes para señalar.
Realiza tantas figuras geométricas hasta que el número de partes del numerador pueda ser señalado.

– Grafica la fracción $\frac{10}{6}$

Primero se divide la figura en 6 partes iguales:

Como el numerador es igual a 10, nos hace falta otra figura idéntica para completar las 10 partes que se van a seleccionar. Recuerda que se pueden agregar tantas figuras como sean necesarias hasta poder representar el número de partes del numerador.

Como las fracciones impropias tienen el numerador mayor al denominador, siempre van a estar representadas con más de una figura, porque representan a “algo” mayor que la unidad. Por esta razón, las fracciones de este tipo también pueden representarse como números mixtos. Por ejemplo la fracción 10/6 en número mixto se representa como 1 4/6.

Problemas cotidianos

Expresiones como “un cuarto de hora”, “media taza de té”, “tres cuartas partes de la población”, son algunos ejemplos en los que se emplean las fracciones dentro del lenguaje cotidiano. Por eso es común encontrarnos con fracciones y resolver problemas habituales. Algunos ejemplos son los siguientes:

– En una escuela solo la cuarta parte de los estudiantes practica fútbol, ¿cuál sería la representación gráfica de esa proporción?

Las expresión “cuarta parte” hace referencia a la fracción un cuarto: $\frac{1}{4}$ . Entonces, lo que debemos hacer es graficar dicha fracción y responder así la interrogante del problema:

– En una fiesta compraron 3 pizzas del mismo tamaño que estaban cortadas en 4 partes iguales cada una. Uno de los invitados se comió una de las porciones, ¿cómo se puede expresar en forma de fracción al número de porciones de pizza que quedaron?

Lo primero que tenemos que hacer es imaginarnos las pizzas con el número total de porciones:

De la imagen determinamos que originalmente habían 12 porciones. Luego tenemos que imaginar cuántas porciones quedaron después de que el invitado se comiera una de ellas:

La imagen anterior representaría la gráfica del problema, ahora lo que debemos hacer es determinar la fracción de ella. Recordemos que el denominador es el número en el que se divide la unidad, en este caso la unidad es cada pizza y cada una de ellas está cortada o dividida en cuatro porciones, por lo tanto, el denominador es 4.

Como el numerador es el número de partes que se considera de la unidad, en este caso serían las porciones que quedaron, por lo tanto, el numerador es 11.

De esta manera se concluye que quedaron $\frac{11}{4}$ de porciones de pizza.

Observa que $\frac{11}{4}$ es una fracción impropia y por eso la unidad (la pizza) fue graficada más de una vez.

¡A practicar!

1. ¿Qué fracción representan las siguientes gráficas?

Solución

$\frac{2}{6}$

Solución

$\frac{3}{4}$

Solución

$\frac{5}{7}$

Solución

$\frac{2}{4}$

Solución

$\frac{7}{3}$

Solución

$\frac{2}{2}$

2. ¿Cuál de las siguientes expresiones representa al siguiente gráfico?

a) Un quinto de taza de café.
b) Cinco medios de cucharadas de azúcar.
c) Tres medios de harina.
d) Tres quintas partes de agua.
e) Dos terceras partes de vinagre.

Solución

d) Tres quintas partes de agua $\left ( \frac{3}{5} \right )$ .

RECURSOS PARA DOCENTES

Artículo “Fracciones”

El presente artículo destacado explica los elementos de una fracción y la forma de graficarlas de acuerdo a sus tipos. También presenta una serie de ejemplos que facilitan su comprensión.

VER

Enciclopedia “Recursos para docentes”

La enciclopedia muestra algunas herramientas para ayudar el proceso de aprendizaje de los estudiantes en todas las áreas de estudio.

VER