Etiqueta: inpropias

CAPÍTULO 3 / TEMA 3

Gráficas de fracciones

Las gráficas son recursos visuales que permiten representar datos numéricos, como las fracciones. En este tipo de problemas podemos usar gran variedad de figuras para expresar una fracción de manera más sencilla, y así facilitar su interpretación. Los pasos para poder graficar una fracción dependen de su tipo.

Graficar una fracción propia

Podemos expresar fracciones a través de diagramas, pero para comprender cómo realizar un gráfico es importante recordar que una fracción es la representación de una o varias partes iguales de la unidad, donde:

El denominador representa el número de partes que se dividen de la unidad.

El numerador es el número de partes que se toman o se consideran de la unidad.

Toda fracción propia cumple una condición: el numerador siempre es menor que el denominador.

Pasos para graficar una fracción propia

  1. Elige la figura en la que se va a representar la fracción. Puede ser un triángulo, círculo, cuadrado, rectángulo, etc.
  2. Divide la figura elegida en tantas partes como indique el denominador de la fracción. Todas las partes deben ser iguales.
  3. Señala el número de partes que indique el numerador de la fracción.

– Grafica la fracción \frac{3}{4}

La figura que seleccionaremos en este caso será un triángulo, pero recuerda que puede ser cualquier figura. Como el denominador de la fracción es cuatro (4), la figura debe estar dividida en cuatro partes iguales:

Luego señalamos el número de partes que indique el numerador, en este caso serían tres (3) partes:

De manera gráfica es más fácil entender la representación de la fracción “tres cuartos”.

Otros ejemplos:

¿Sabías qué?
Las fracciones no solo pueden representarse con figuras geométricas, también lo pueden hacer en la recta numérica.

¿Cómo graficar fracciones cuyo numerador es igual al denominador?

A este tipo de fracción se lo denomina fracción igual la unidad porque, al ser iguales el numerador y el denominador, el cociente de ambos siempre va a ser uno (1). Por esta razón la representamos como toda la figura geométrica:

VER INFOGRAFÍA

Graficar una fracción impropia

En las fracciones impropias el numerador siempre es mayor al denominador y, como su resultado es mayor a la unidad, se requiere más de una figura geométrica para representarlas.

Pasos para graficar una fracción impropia

  1. Elige la figura en la que se va a representar la fracción.
  2. Divide la figura elegida en tantas partes como indique el denominador de la fracción. Todas las partes deben ser iguales.
  3. Señala el número de partes que indique el numerador de la fracción. Como es una fracción impropia van a faltar partes para señalar.
  4. Realiza tantas figuras geométricas hasta que el número de partes del numerador pueda ser señalado.

– Grafica la fracción \frac{10}{6}

Primero se divide la figura en 6 partes iguales:

Como el numerador es igual a 10, nos hace falta otra figura idéntica para completar las 10 partes que se van a seleccionar. Recuerda que se pueden agregar tantas figuras como sean necesarias hasta poder representar el número de partes del numerador.

Como las fracciones impropias tienen el numerador mayor al denominador, siempre van a estar representadas con más de una figura, porque representan a “algo” mayor que la unidad. Por esta razón, las fracciones de este tipo también pueden representarse como números mixtos. Por ejemplo la fracción 10/6 en número mixto se representa como 1 4/6.

 

Problemas cotidianos

Expresiones como “un cuarto de hora”, “media taza de té”, “tres cuartas partes de la población”, son algunos ejemplos en los que se emplean las fracciones dentro del lenguaje cotidiano. Por eso es común encontrarnos con fracciones y resolver problemas habituales. Algunos ejemplos son los siguientes:

– En una escuela solo la cuarta parte de los estudiantes practica fútbol, ¿cuál sería la representación gráfica de esa proporción?

Las expresión “cuarta parte” hace referencia a la fracción un cuarto: \frac{1}{4}. Entonces, lo que debemos hacer es graficar dicha fracción y responder así la interrogante del problema:

– En una fiesta compraron 3 pizzas del mismo tamaño que estaban cortadas en 4 partes iguales cada una. Uno de los invitados se comió una de las porciones, ¿cómo se puede expresar en forma de fracción al número de porciones de pizza que quedaron?

Lo primero que tenemos que hacer es imaginarnos las pizzas con el número total de porciones:

De la imagen determinamos que originalmente habían 12 porciones. Luego tenemos que imaginar cuántas porciones quedaron después de que el invitado se comiera una de ellas:

La imagen anterior representaría la gráfica del problema, ahora lo que debemos hacer es determinar la fracción de ella. Recordemos que el denominador es el número en el que se divide la unidad, en este caso la unidad es cada pizza y cada una de ellas está cortada o dividida en cuatro porciones, por lo tanto, el denominador es 4.

Como el numerador es el número de partes que se considera de la unidad, en este caso serían las porciones que quedaron, por lo tanto, el numerador es 11.

De esta manera se concluye que quedaron \frac{11}{4} de porciones de pizza.

Observa que \frac{11}{4} es una fracción impropia y por eso la unidad (la pizza) fue graficada más de una vez.

¡A practicar!

1. ¿Qué fracción representan las siguientes gráficas?

a)

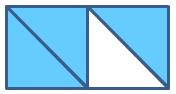
Solución
\frac{2}{6}
b) 
Solución
\frac{3}{4}
c) 
Solución
\frac{5}{7}
d) 
Solución
\frac{2}{4}
e) 
Solución
\frac{7}{3}
e) 
Solución
\frac{2}{2}

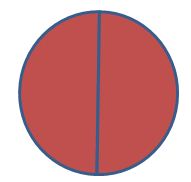
2. ¿Cuál de las siguientes expresiones representa al siguiente gráfico?


a) Un quinto de taza de café.
b) Cinco medios de cucharadas de azúcar.
c) Tres medios de harina.
d) Tres quintas partes de agua.
e) Dos terceras partes de vinagre.

Solución
d) Tres quintas partes de agua \left ( \frac{3}{5} \right ).

RECURSOS PARA DOCENTES

Artículo “Fracciones”

El presente artículo destacado explica los elementos de una fracción y la forma de graficarlas de acuerdo a sus tipos. También presenta una serie de ejemplos que facilitan su comprensión.

VER

Enciclopedia “Recursos para docentes”

La enciclopedia muestra algunas herramientas para ayudar el proceso de aprendizaje de los estudiantes en todas las áreas de estudio.

VER

CAPÍTULO 3 / TEMA 2

Fracciones diversas

Las fracciones pueden clasificarse en dos grupos: fracciones propias y fracciones impropias. Estas clasificaciones dependen de la relación que exista entre el numerador y el denominador. Por otro lado, el denominador de una fracción también permite compararla con otra para saber si es homogénea o heterogénea.

Fracciones propias e impropias

Una fracción propia es aquella donde el denominador es mayor que el numerador. A este tipo de fracción también se la conoce como fracción pura. Las siguientes fracciones son ejemplos de fracciones propias o puras:

\frac{1}{8}; \frac{5}{33}; \frac{9}{10}; \frac{97}{99}

Al dividir el numerador entre el denominador de una fracción propia el resultado siempre estará comprendido entre cero (0) y uno (1), es decir:

\frac{1}{8}= 0,125

\frac{5}{33}=0,\widehat{15}

\frac{1}{9} = 0,\widehat{1}

\frac{97}{99}=0,\widehat{97}

 

¿Sabías qué?
De acuerdo a cada país se pueden usar los términos fracción propia o pura e impropia o impura para referirse a los mismos tipos de fracciones.

Una fracción impropia es aquella cuyo numerador siempre es mayor que el denominador. Se la conoce también como fracción impura y algunos ejemplos son los siguientes:

\frac{5}{2}; \frac{7}{3}; \frac{14}{5}; \frac{3}{2}

Al dividir el numerador entre el denominador de una fracción impropia el resultado siempre será mayor a uno (1). Por ejemplo:

\frac{5}{2}=2,5

\frac{7}{3}=2,\widehat{3}

\frac{14}{5}=2,8

\frac{3}{2}=1,5

 

Fracciones aparentes

Son fracciones en las cuales la división entre el numerador y denominador es igual a un número entero. La fracción \frac{8}{2} es una fracción aparente porque 8 ÷ 2 = 4 y el cuatro (4) es un número entero. Las fracciones aparentes se distinguen porque el numerador siempre es un múltiplo del denominador.

Fracciones homogéneas y heterogéneas

Como ya sabemos, el denominador en una fracción determina en cuántas partes está dividido el entero. Sin importar su numerador, dos fracciones son homogéneas si comparten el mismo denominador:

\frac{1}{3} y \frac{2}{3} son fracciones homogéneas porque su denominador es el mismo: 3. En las fracciones homogéneas el entero se ha dividido por la misma cantidad de partes:

Por otro lado, dos fracción son heterogéneas si sus denominadores son diferentes, es decir, el entero se dividió en partes diferentes para cada caso:

¿Qué es una fracción equivalente?

Equivalente quiere decir “de igual valor”, en este sentido, las fracciones equivalentes son aquellas que representan la misma cantidad. Las fracciones \frac{1}{2}; \frac{2}{4} y \frac{3}{6} son equivalentes:

Pasos para determinar si dos fracciones son equivalentes

1. Multiplica el numerador de la primera fracción por el denominador de la segunda.

2. Multiplica el numerador de la segunda fracción por el denominador de la primera.

3. Si los productos anteriores son iguales, entonces las fracciones son equivalentes.

– Determina si las fracciones \frac{1}{3} y \frac{3}{9} son equivalentes.

Lo primero que debemos hacer es multiplicar el numerador de la primera fracción que es 1 por el denominador de la segunda fracción que es 9. Luego multiplicamos el numerador de la segunda fracción que es 3 por el denominador de la primera fracción que también es 3.

En este caso ambas fracciones son equivalentes porque los productos cruzados son iguales.

– Determina si las fracciones \frac{2}{5} y \frac{3}{4} son equivalentes.

Realizamos los productos cruzados y comparamos los resultado:

Como el producto cruzado dio diferente, entonces, las fracciones no son equivalentes.

Existen otras maneras para comprobar fracciones equivalentes, una de las más conocidas es transformar las fracciones a decimales, es decir; dividir el numerador de cada una entre su denominador correspondiente, ambos resultados deben ser iguales para que sean consideradas fracciones equivalentes; por ejemplo; 1/2 y 2/4 son equivalentes porque 1 ÷ 2 = 0,5 y 2 ÷ 4 =0,5.
¡A practicar!

1. Determina si la fracción mostrada es propia o impropia.

a) \frac{23}{40}

Solución
Propia.

b) \frac{3}{2}

Solución
Impropia.

c) \frac{2}{5}

Solución
Propia.

d) \frac{12}{11}

Solución
Impropia.

2. Determina si las siguientes fracciones son homogéneas o heterogéneas.

a) \frac{7}{10} y \frac{9}{10}

Solución
Son fracciones homogéneas.

b) \frac{11}{6} y \frac{14}{9}

Solución
Son fracciones heterogéneas.

c) \frac{13}{4} y \frac{9}{4}

Solución
Son fracciones homogéneas.

d) \frac{58}{7} y \frac{58}{17}

Solución
Son fracciones heterogéneas.

3. ¿Cuál de las siguientes fracciones es equivalente a \frac{5}{2}?

a) \frac{2}{5}

b) \frac{10}{2}

c) \frac{52}{10}

d) \frac{15}{6}

Solución
d) \frac{15}{6}

RECURSOS PARA DOCENTES

Artículo “Clasificación de fracciones”

Este artículo destacado trata sobre las características principales de las fracciones y los diferentes criterios para clasificarlas. También se muestran una serie de ejemplos que facilitan su comprensión.

VER

Micrositio “Tarjetas educativas – Operaciones matemáticas”

En el siguiente micrositio se presentan las principales operaciones matemáticas, especialmente las operaciones básicas realizadas con fracciones.

VER

Video “Fracciones decimales”

Este video permite convertir números decimales en fracciones y con ello se puede establecer una relación con las fracciones propias.

VER