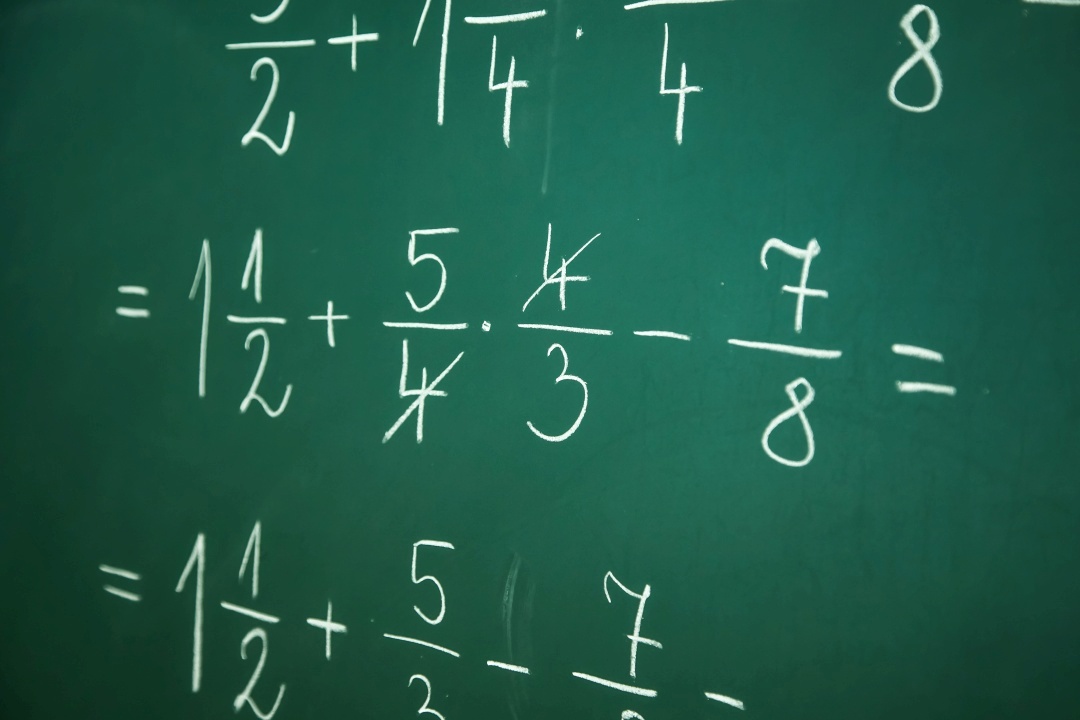Mínimo común múltiplo Y Máximo común divisor
Todo número natural se puede descomponer con la multiplicación de sus factores o números primos. La utilidad para descomponerlos de esta manera es que nos permitirá calcular el mínimo común múltiplo y el máximo común divisor de dos o más números. Y con ellos resolver diversos problemas.
mínimo común múltiplo Y Máximo común divisor
El mínimo común múltiplo (mcm), también conocido como múltiplo común menor de dos o más números naturales, es el menor múltiplo común de ambos números que sea distinto de cero.
El máximo común divisor (mcd), también conocido como divisor común mayor entre dos o más números naturales, es el mayor divisor entre ambos, es decir, el mayor número por el que son divisibles dos o más números.
CÁLCULO DEL Mínimo común múltiplo
Para calcular el mcm entre dos o más números podemos seguir los siguientes pasos:
- Descomponer los números en sus factores primos.
- Escribir los números como la multiplicación de sus factores primos.
- Escribir en en la parte inferior el mcm que será igual al producto de todos los factores comunes y no comunes de los números a la mayor potencia. Es decir, si entre los números a los que se le realizó la descomposición se observa un factor que se repite pero con exponente diferente, se considera el que tiene el mayor exponente.
- Resolver el producto del mcm.
Por ejemplo:
-Hallar el mcm entre 40 y 60.
Lo primero es descomponer los dos números en factores primos y expresar dicha descomposición en forma de multiplicación:
Luego se eligen los factores comunes y no comunes. En el caso del 2, está en ambas expresiones con diferente exponente, en este caso se considera el 23 porque es mayor. De esta forma, el mcm de ambos números es:
mcm (40, 60) = 23 · 3 · 5
Al resolver el producto obtenido el resultado es:
mcm (40, 60) = 23 · 3 · 5 = 2 · 2 · 2 ·3 · 5 = 120
De esta forma, el mínimo común múltiplo entre 40 y 60 es 120.
CÁLCULO DEL Máximo común divisor
Para calcular el mcd entre dos o más números se pueden seguir los siguientes pasos:
- Descomponer los números en sus factores primos.
- Escribir los números como la multiplicación de sus factores primos.
- Escribir en la parte inferior el mcd que será igual al producto de los factores que tienen en común a la menor potencia. Es decir, si se repite un factor se considera el que tiene la menor potencia.
- Resolver el producto del mcd.
Por ejemplo:
-Hallar el mcd entre 56 y 48.
Primero se descomponen ambos números en sus factores primos:
Luego se seleccionan únicamente los factores que tienen en común. En este caso, el factor en común entre ambos números es el 2 que se encuentra expresado en diferente potencia: 23 y 24. Para calcular el mcd se toma únicamente la menor potencia, en este caso sería 23. De esta manera, el mcd queda expresado de la siguiente manera:
mcd (56, 48) = 23
Al resolver la potencia se obtiene el resultado:
mcd (56, 48) = 8
De esta manera, el mcd entre 56 y 48 es el número 8.
El mcd de los números de Fibonacci
Los números de la secuencia de Fibonacci son: 1, 1, 2, 3, 5, 8, 13, 21, 34, 89 y siguen hasta el infinito. Esta secuencia consiste en sumar los dos números anteriores para hallar el siguiente número. Por ejemplo, 1 + 1 = 2, 2 + 1 = 3, 2 + 3 = 5, y así sucesivamente hasta el infinito.
Lo curioso de estos números es que si calculamos el máximo común divisor de dos números de Fibonacci obtenemos otro número de la secuencia de Fibonacci. Por ejemplo, el mcd (3, 21) = 3.
problemas de aplicación
Para resolver problemas de mcm y mcd hay que tener en cuenta los datos del problema y la pregunta que nos hace, en ella estará la clave para saber si el problema se resuelve con mcm y mcd. Veremos unos ejemplos donde se tenga que aplicar alguno de los dos cálculos:
1. En una ciudad, el reloj de la catedral indica la hora a través de campanadas que suenan cada 3 horas, y el reloj de la torre de la plaza lo hace cada 8 horas. ¿Cada cuántas horas ambos relojes sonarán al mismo tiempo?
Los datos del problema indican que el reloj de la catedral suena cada 3 horas y el de la municipalidad cada 8 horas. Al descomponer ambos números se obtiene:
En este caso, se trata de un problema de mínimo común múltiplo, y se debe calcular el mismo entre ambos números para determinar cada cuántas horas sonarán al mismo tiempo los relojes.
mcm (3, 8) = 3 · 23
mcm (3, 8) = 24
De esta manera, se determinó que los relojes suenan al mismo tiempo cada 24 horas.
2. En la tienda de Jorge hay una caja con 12 naranjas y otra con 18 peras. Jorge quiere distribuir las frutas en cajas más pequeñas de forma que todas las cajas tengan la misma cantidad de fruta. Cada caja solo puede tener peras o naranjas y las cajas deben ser lo más grande posible. ¿Cuántas frutas debe haber en cada caja?
Los datos del problema son cajas de 12 naranjas y 18 peras. Al descomponer dichos números en factores primos se obtiene:
En este problema debemos separar o dividir las frutas en diferentes cajas, por lo tanto se resuelve a través del mcd.
mcd (12, 18) = 2 · 3
mcd (12, 18) = 6
De esta manera, se determinó que en cada caja debe haber 6 frutas.
¡A practicar!
- Calcula el mínimo común múltiplo entre los siguientes números.
a) 30, 60 y 90
mcm (30,60,90) = 23 . 32 . 5 = 180
b) 15, 30, 20 y 40
mcm (15,30,20,40) = 23 . 3 . 5 = 120
2. Calcula el máximo común divisor entre los siguientes números.
a) 18, 26 y 40
mcd (18,26,40) = 2
b) 54, 60, 80 y 100
mcd (54,60,80,100) = 2
3. Marcos tiene una cuerda de 120 metros y otra de 96 metros. Desea cortarlas de modo que todos los trozos sean iguales pero lo más largos posible. ¿Cuánto medirá cada trozo de cuerda?
mcd (120,96) = 23 . 3 = 24
Cada trozo medirá 24 metros.
4. Un jardinero riega el césped de un parque cada 5 días y lo corta cada 8 días. ¿Cada cuántos días coincidirán sus funciones de riego y de corte del césped?
mcm (5,8) = 23 . 5 = 40
Las funciones de riego y corte de césped coincidirán cada 40 días.
5. Una tienda compra memorias USB de diferentes colores. Para Navidad hizo un pedido de 84 memorias rojas, 196 azules y 252 verdes. Para guardar la mercancía de forma organizada, exigió que le enviaran las memorias en cajas iguales, sin mezclar los colores y con el mayor número posible de memorias. ¿Cuántas memorias habrá en cada caja?
mcd (84,196,252) = 22 . 7 = 4 . 7 = 28
En cada caja habrá 28 memorias.
6. Adrián es un deportista de alto rendimiento que practica después del colegio. Cada 3 días recorre un trayecto en bicicleta por la ciudad, cada 4 días juega fútbol y cada 12 días juega al hockey. ¿Cuántos días pasarán para que realice las tres actividades en el mismo día?
mcm (3,4,12) = 22 . 3 = 4 . 3 = 12
Pasarán 12 días para que haga las tres actividades el mismo día.
