FUNCIONES
Una función es una relación entre variables en la que cada valor de una variable corresponde a un único valor de la otra. Por ejemplo, el peso en kilogramos de manzanas y el precio del kilogramo de ese producto son magnitudes relacionadas que representan una función, pues a cada número de kilogramos le corresponde un precio específico. La forma en las que las variables se relacionan determina el tipo de función.

¿QUÉ ES UNA FUNCIÓN?
Es una expresión que indica una relación de correspondencia entre dos conjuntos. Siempre se debe cumplir que todo elemento del conjunto de partida tenga una única relación con algún elemento del conjunto de llegada.
- Conjunto: es el grupo de elementos que no se repiten.
- Dominio: es el conjunto de partida. Lo denotamos como Dom f.
- Rango: son los elementos del codominio que se obtienen al aplicar la función. Se abrevia Rg f.
- Codominio: es el conjunto de llegada. Se denota como Codom f.
Si denotamos al conjunto de partida con la letra A, al de llegada con la letra B y a la función que los relaciona con f, entonces, el diagrama sagital para indicar la relación entre A y B, sería:

Esta función se puede expresar como:
f: A → B = {(a, 3), (b, 2), (c, 6), (d, 1), (e, 4)}
Donde el dominio y el rango son:
Dom f = {a, b, c, d, e}
Rg f = {1, 2, 3, 4, 5, 6}
Si alguno de los elementos del conjunto de partida no tiene imagen en el conjunto de llegada, o bien, si posee más de una imagen en el conjunto de llegada, serían relaciones, pero no son funciones. Por ejemplo:

Esta relación no corresponde a la definición de función, ya que hay un elemento del conjunto de partida (a) que no tiene ninguna imagen en el conjunto de llegada.

Esta relación tampoco es una función, ya que un elemento del conjunto de partida (d) que tienen dos imágenes diferentes en el conjunto de llegada (1 y 5).

¿Cómo representar una función?
Existen diversas maneras de representar funciones matemáticas, entre ellas, las más comunes son las siguientes:
| Diagrama sagital | Forma algebraica | Gráfico de la función |
| Es un gráfico compuesto por formas cerradas que representan los conjuntos que se relacionan a través de flechas. | Es la expresión algebraica de la función. | Es la relación gráfica de ambas variables. Cada eje representa un conjunto y la unión de los puntos muestra el comportamiento de la función. |
 |
 |
TIPOS DE FUNCIONES
Función inyectiva
Es una función en la cual a cada elemento del rango le corresponde una única imagen en el dominio o conjunto de partida.
– Ejemplo:
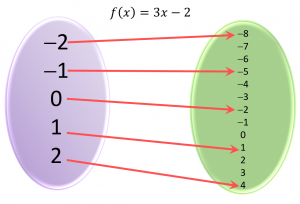
f(x) = 3x − 2
Evaluada en los números enteros , para:
x = −2, −1, 0, 1, 2
Al sustituir en f(x) = 3x − 2, tenemos:
f(−2) = 3(−2) − 2 = −8
f(−1) = 3(−1) − 2 = −5
f(0) = 3(0) − 2 = −2
f(1) = 3(1) − 2 = 1
f(2) = 3(2) − 2 = 4
Así que podemos expresar:
Dom f = {−2, −1, 0, 1, 2}
Rg f = {−8, −5, −2, 1, 4}
Función sobreyectiva
Una función es sobreyectiva cuando cada elemento del rango es imagen de al menos un elemento del dominio.
– Por ejemplo:
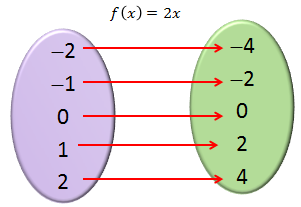
f(x) = 2x
Evaluada en los números enteros , para:
x = −2, −1, 0, 1, 2
Sustituyendo en f(x) = 2x, tenemos:
f(-2) = 2(−2) = −4
f(−1) = 2(−1) = −2
f(0) = 2(0) = 0
f(1) = 2(1) = 2
f(2) = 2(2) = 4
Podemos expresar:
Dom f = {−2, −1, 0, 1, 2}
Rg f = {−4, −2, 0, 2, 4}
El diagrama sagital para el dominio y rango de la función sería:
Función biyectiva
Una función es biyectiva, cuando es inyectiva y sobreyectiva a la vez.

– Ejemplo:
f(x) = x
Evaluada en los números enteros , para:
x = −2, −1, 0, 1, 2
Al sustituir en f(x) = x, tenemos:
f(−2) = −2 = −2
f(−1) = −1 = −1
f(0) = 0 = 0
f(1) = 1 = 1
f(2) = 2 = 2
Podemos expresar:
Dom f = {−2, −1, 0, 1, 2}
Rg f = {−2, −1, 0, 1, 2}

Otra clasificación
Si ahora clasificamos las funciones de acuerdo con los operadores matemáticos que contienen, podemos agrupar las funciones en algunas de las siguientes categorías:
- Funciones polinómicas: son funciones compuestas por la suma o resta de términos que tienen la forma ax2, conocidos como monomios, por ejemplo:
f(x) = −6x4 + 11x3 − 7x2 − x − 5
- Funciones logarítmicas: son funciones que contienen entre sus términos al logaritmo, por ejemplo:
f(x) = logax, para a ˃ 1, y 0 ˂ a ˂ 1
La función logarítmica es la inversa de la función exponencial.
- Funciones exponenciales: son aquellas que están formadas por una base constante y la variable independiente se encuentra en el exponente, digamos:
f(x) = −125x
- Funciones trigonométricas: son las que se caracterizan por contener funciones trigonométricas en al menos uno de sus términos, por ejemplo:
f(x) = 9 · cos(−6x2) + sen2(8x) = 17
FUNCIONES EN LA VIDA COTIDIANA

Son infinitas las utilidades que tienen las funciones tanto en la vida diaria como en ciertas áreas del conocimiento, que van desde las ciencias exactas, hasta la medicina y las ciencias naturales. A continuación, te mencionamos algunos ejemplos:
- Para describir el movimiento de un cuerpo. Por ejemplo, si estudiamos el movimiento de un vehículo que se desplaza por una carretera recta, podemos determinar la distancia horizontal a la que se encuentra de un origen en cualquier instante de tiempo. Esto es posible mediante una ecuación polinómica que describe la posición horizontal de una partícula en función del tiempo.
- Para determinar el crecimiento demográfico. Algunas poblaciones muestran crecimientos que los científicos has demostrado que obedecen a funciones exponenciales. Mediante dichas funciones es posible estimar la cantidad de habitantes que habrá en una zona en un determinado periodo de tiempo.
- Para saber la velocidad de reproducción de colonias de bacterias. Muchas colonias de bacteria se reproducen a una tasa exponencial, por lo que si se determina la función que describe este comportamiento, los científicos pueden calcular la cantidad de colonias de bacterias en un espacio y tiempo específico.
¡A practicar!
1. Indique si la siguiente relación de conjuntos es una función. Justifique su respuesta.

2. Evalúa la función f(x) = 5x − 4 para el conjunto de los números enteros en el dominio Dom f = {−2, −1, 0, 1, 2}, e indica si es una función inyectiva, sobreyectiva o biyectiva.
























































































